题目内容
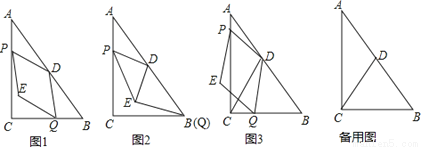
如图1,Rt△ABC中,∠ACB=Rt∠,AC=8,BC=6,点D为AB的中点,动点P从点A出发,沿AC方向以每秒1个单位的速度向终点C运动,同时动点Q从点C出发,以每秒2个单位的速度先沿CB方向运动到点B,再沿BA方向向终点A运动,以DP,DQ为邻边构造?PEQD,设点P运动的时间为t秒.
(1)当t=2时,求PD的长;
(2)如图2,当点Q运动至点B时,连结DE,求证:DE∥AP.
(3)如图3,连结CD.
①当点E恰好落在△ACD的边上时,求所有满足要求的t值;
②记运动过程中?PEQD的面积为S,?PEQD与△ACD的重叠部分面积为S1,当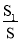 <
<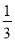 时,请直接写出t的取值范围是 ______ .
时,请直接写出t的取值范围是 ______ .
练习册系列答案
相关题目


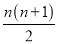 .
.
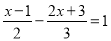 时,去分母正确的是( )
时,去分母正确的是( )