题目内容
18.用配方法解方程2x2+3=7x时,方程可变形为( )| A. | (x-$\frac{7}{4}$ )2=$\frac{25}{16}$ | B. | (x-$\frac{7}{4}$)2=$\frac{73}{16}$ | C. | (x-$\frac{3}{4}$ )2=$\frac{65}{16}$ | D. | (x-$\frac{7}{2}$)2=$\frac{25}{16}$ |
分析 利用配方法将方程变形,即可作出判断.
解答 解:方程整理得:x2-$\frac{7}{2}$x=-$\frac{3}{2}$,
配方得:x2-$\frac{7}{2}$x+$\frac{49}{16}$=$\frac{25}{16}$,即(x-$\frac{7}{2}$)2=$\frac{25}{16}$,
故选D
点评 此题考查了一元二次方程-配方法,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
8.下列说法正确的是( )
(1)-2是-8的立方根;
(2)16的算术平方根是4;
(3)+3和-3都是27的立方根;
(4)64的平方根是8.
(1)-2是-8的立方根;
(2)16的算术平方根是4;
(3)+3和-3都是27的立方根;
(4)64的平方根是8.
| A. | (1)和(3) | B. | (3)和(4) | C. | (2)和(4) | D. | (1)和(2) |
6.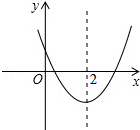 如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列4个结论:
如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列4个结论:
①a>0;②b<0;③b<a+c;④4a+2b+c>0其中正确结论的有( )
 如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列4个结论:
如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列4个结论:①a>0;②b<0;③b<a+c;④4a+2b+c>0其中正确结论的有( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
3.下列图形中,既是轴对称图形又是中心对称图形的( )
| A. |  | B. |  | C. |  | D. |  |
7.要使式子$\frac{\sqrt{a-2}}{a-3}$有意义,a的取值范围是( )
| A. | a≠3 | B. | a>2且a≠3 | C. | a≥2或a≠3 | D. | a≥2且a≠3 |



