题目内容
13.(1)$\frac{\sqrt{18}×\sqrt{2}}{\sqrt{3}}$(2)${({\sqrt{2}+\sqrt{5}})^2}$
(3)$3\sqrt{8}-4\sqrt{32}$
(4)$({\sqrt{18}-\sqrt{\frac{1}{2}}})×\sqrt{8}$
(5)2-$\frac{{\sqrt{27}-\sqrt{12}}}{{\sqrt{3}}}$
(6)$\sqrt{32}-3\sqrt{\frac{1}{2}}+\sqrt{2}$
(7)$\sqrt{40}×\sqrt{10}-21$.
分析 (1)按照二次根式的运算法则进行计算,再化简,即可得出结论;
(2)将平方展开,再按照二次根式的运算法则进行计算,即可得出结论;
(3)将二次根式化简,化简后按照实数加减法的运算法则进行计算,即可得出结论;
(4)按照二次根式的运算法则进行计算,再化简,即可得出结论;
(5)按照二次根式的运算法则进行计算,再化简,即可得出结论;
(6)将二次根式化简,化简后按照实数加减法的运算法则进行计算,即可得出结论;
(7)将二次根式化简,化简后按照实数加减法的运算法则进行计算,即可得出结论.
解答 解:(1)$\frac{\sqrt{18}×\sqrt{2}}{\sqrt{3}}$=$\sqrt{18×2÷3}$=$\sqrt{12}$=2$\sqrt{3}$.
(2)${(\sqrt{2}+\sqrt{5})}^{2}$=${(\sqrt{2})}^{2}$+${(\sqrt{5})}^{2}$+2$\sqrt{2×5}$=7+2$\sqrt{10}$.
(3)3$\sqrt{8}$-4$\sqrt{32}$=6$\sqrt{2}$-16$\sqrt{2}$=-10$\sqrt{2}$.
(4)($\sqrt{18}$-$\sqrt{\frac{1}{2}}$)×$\sqrt{8}$=$\sqrt{18×8}$-$\sqrt{8÷2}$=12-2=10.
(5)2-$\frac{\sqrt{27}-\sqrt{12}}{\sqrt{3}}$=2-$\sqrt{27÷3}$+$\sqrt{12÷3}$=2-3+2=1.
(6)$\sqrt{32}$-3$\sqrt{\frac{1}{2}}$+$\sqrt{2}$=4$\sqrt{2}$-$\frac{3}{2}$$\sqrt{2}$+$\sqrt{2}$=$\frac{7}{2}$$\sqrt{2}$.
(7)$\sqrt{40}$×$\sqrt{10}$-21=$\sqrt{40×10}$-21=20-21=-1.
点评 本题考查了二次根式的混合运算,解题的关键是牢记二次根式的运算规则以及二次根式化简的方法.

| A. | 袋中装有一个红球和两个白球,它们除颜色外都相同,从中随机地摸出一个球,记下颜色后放回,充分摇动后,再从中随机地摸出一个球,两次摸到不同颜色球的概率是$\frac{4}{9}$ | |
| B. | 甲、乙两人玩“石头、剪刀、布”的游戏,游戏规则是:如果两人的手势相同,那么第三人丙获胜,如果两人手势不同,按照“石头胜剪刀,剪刀胜布,布胜石头”的规则决定甲、乙的获胜者.这个游戏规则对于甲、乙、丙三人是公平的 | |
| C. | 连续抛两枚质地均匀的硬币,“两枚正面朝上”、“两枚反面朝上”和“一枚正面朝上,一枚反面朝上”,这三种结果发生的概率是相同的 | |
| D. | 一个小组的八名同学通过依次抽签(卡片外观一样,抽到不放回)决定一名同学获得元旦奖品,先抽和后抽的同学获得奖品的概率是相同的,抽签的先后不影响公平 |

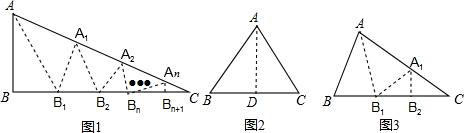

 如图,在△ABC中,AD⊥BC于D,AD=BC=12,点P在AB上,且PQ∥AD交BC于点Q,PM∥BC交AC于点M,若PM=2PQ,则PM等于( )
如图,在△ABC中,AD⊥BC于D,AD=BC=12,点P在AB上,且PQ∥AD交BC于点Q,PM∥BC交AC于点M,若PM=2PQ,则PM等于( )