题目内容
9.以点A(1,-2)为中心,把点B(0,2)顺时针旋转90°,得到点C,则点C的坐标为(3,-3).分析 如图作AE⊥OB,CM⊥OB,AF⊥CM垂足分别为E、M、F,利用△AEB≌△AFC即可解决问题.
解答 解:如图作AE ⊥OB,CM⊥OB,AF⊥CM垂足分别为E、M、F.
⊥OB,CM⊥OB,AF⊥CM垂足分别为E、M、F.
∵∠AEM=∠EMF=∠AFM=90°,
∴四边形AEMF是矩形,
∴∠EAF=90°,AE=FM=2
∵∠BAC=90°,
∴∠EAF=∠BAC,
∴∠EAB=∠FAC,
在△AEB和△AFC中,
$\left\{\begin{array}{l}{∠EAB=∠FAC}\\{∠AEB=∠AFC}\\{AB=AC}\end{array}\right.$,
∴△AEB≌△AFC,
∴AE=AF=2,BE=CF=1,CM=3,
∴点C(3,-3).
故答案为C(3,-3).
点评 本题考查旋转的性质、全等三角形的判定和性质、矩形的判定和性质等知识,构造全等三角形是解决问题的关键.

练习册系列答案
相关题目
20.计算4x3•x2的结果是( )
| A. | 4x6 | B. | 4x5 | C. | 4x4 | D. | 4x3 |
4.已知圆锥的母线长为5cm,高为4cm,则这个圆锥的侧面积为( )
| A. | 12πcm2 | B. | 15πcm2 | C. | 20πcm2 | D. | 25πcm2 |
18.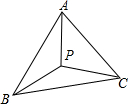 如图,已知△APB和△APC是以AP所在的直线为对称轴的轴对称图形,若PA=PB,∠PAB=30°,则∠BPC的大小是( )
如图,已知△APB和△APC是以AP所在的直线为对称轴的轴对称图形,若PA=PB,∠PAB=30°,则∠BPC的大小是( )
 如图,已知△APB和△APC是以AP所在的直线为对称轴的轴对称图形,若PA=PB,∠PAB=30°,则∠BPC的大小是( )
如图,已知△APB和△APC是以AP所在的直线为对称轴的轴对称图形,若PA=PB,∠PAB=30°,则∠BPC的大小是( )| A. | 110° | B. | 130° | C. | 120° | D. | 140° |

 己知,如图,在△ABC中,∠C=90°,∠A=24°,请用直尺和圆规找到一条直线,把△ABC恰好分割成两个等腰三角形(不写作法,但需保留作图痕迹),直线CD即为所求.
己知,如图,在△ABC中,∠C=90°,∠A=24°,请用直尺和圆规找到一条直线,把△ABC恰好分割成两个等腰三角形(不写作法,但需保留作图痕迹),直线CD即为所求.
 如图,已知直线a,b被直线c所截,且∠5+∠2=180°,可以判定直线a∥b吗?试着用不同的方法说明你的结论.
如图,已知直线a,b被直线c所截,且∠5+∠2=180°,可以判定直线a∥b吗?试着用不同的方法说明你的结论. 如图,已知点D在点O的北偏西30°方向,当点E在点O的50°方向时,∠DOE=80°.
如图,已知点D在点O的北偏西30°方向,当点E在点O的50°方向时,∠DOE=80°.