题目内容
4.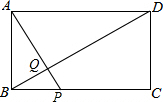 如图,矩形ABCD中,AB=4,BC=10,点P为BC边上一动点,AP交BD于点Q.点P从B点出发沿BC边以每秒1个单位长度的速度向C点移动,移动时间为x秒.设S△AQD+S△PQB=y,写出y与x之间的函数关系式,并探究P点运动到第几秒与第几秒之间时,y取得最小值.( )
如图,矩形ABCD中,AB=4,BC=10,点P为BC边上一动点,AP交BD于点Q.点P从B点出发沿BC边以每秒1个单位长度的速度向C点移动,移动时间为x秒.设S△AQD+S△PQB=y,写出y与x之间的函数关系式,并探究P点运动到第几秒与第几秒之间时,y取得最小值.( )| A. | 3到4 | B. | 4到5 | C. | 5到6 | D. | 6到7 |
分析 因为S△AQD+S△PQB=y,故求S△AQD和S△PQB是解决问题的关键,观察无固定组合规则图象,则考虑作高分别求取.考虑两高在同一直线上,且相加恰为4,故由△AQD∽△PQB结论得,高的比等于对应边长比,设其中一高为h,即可求得,则易表示y,注意要考虑t的取值,探讨得出y最小值.
解答 解:设△PQB的边BP上的高h,则△AQD的边AD上的高为(4-h).
∵AD∥BC,
∴△ADQ∽△BQP,
∴$\frac{h}{4-h}$=$\frac{t}{10}$,
解得 h=$\frac{4t}{10+t}$,
∴4-h=$\frac{40}{10+t}$,
∴S△PQB=$\frac{1}{2}$BP•h=$\frac{2{t}^{2}}{10+t}$,
S△DQA=$\frac{1}{2}$AD(4-h)=$\frac{200}{10+t}$,
∴y=S△AQD+S△PQB=$\frac{2{t}^{2}+200}{10+t}$(0≤t≤10).
探究:
t=0,y=20;
t=1,y≈18.36;
t=2,y≈17.33;
t=3,y≈16.77;
t=4,y≈16.57;
t=5,y=16.67;
t=6,y=17;
t=7,y≈17.53;
t=8,y≈18.22;
t=9,y≈19.05;
t=10,y=20;
观察数据知:
当0≤t≤4时,y随t的增大而减小;
当5≤t≤10时,y随t的增大而增大;
故y在第4秒到第5秒之间取得最小值.
故选:B.
点评 此题考查相似三角形的判定与性质,三角形的面积,函数的最值问题,注意利用三角形的面积计算公式建立函数,进一步求得最值即可.

练习册系列答案
相关题目
16. 如图,矩形ABCD中,AB=$\sqrt{2}$,BC=$\sqrt{3}$,点E是边CD延长线上一点,且DE=1,将△ADE绕点A顺时针旋转后,点E落在直线BC上,则旋转度数是( )
如图,矩形ABCD中,AB=$\sqrt{2}$,BC=$\sqrt{3}$,点E是边CD延长线上一点,且DE=1,将△ADE绕点A顺时针旋转后,点E落在直线BC上,则旋转度数是( )
 如图,矩形ABCD中,AB=$\sqrt{2}$,BC=$\sqrt{3}$,点E是边CD延长线上一点,且DE=1,将△ADE绕点A顺时针旋转后,点E落在直线BC上,则旋转度数是( )
如图,矩形ABCD中,AB=$\sqrt{2}$,BC=$\sqrt{3}$,点E是边CD延长线上一点,且DE=1,将△ADE绕点A顺时针旋转后,点E落在直线BC上,则旋转度数是( )| A. | 30° | B. | 45° | C. | 45°或135° | D. | 75°或165° |
13.已知⊙O的半径为5,直线l上有一点P满足PO=5,则直线l与⊙O的位置关系是( )
| A. | 相切 | B. | 相离 | C. | 相离或相切 | D. | 相切或相交 |
 已知:等边△ABC,边长为8cm,点D从C点出发沿BC方向以1cm/s速度运动,点P从A点出发沿AC方向以2cm/s速度运动,DE∥AC交AB于点E,点D、点P两点同时出发,设运动时间为t s,问:
已知:等边△ABC,边长为8cm,点D从C点出发沿BC方向以1cm/s速度运动,点P从A点出发沿AC方向以2cm/s速度运动,DE∥AC交AB于点E,点D、点P两点同时出发,设运动时间为t s,问: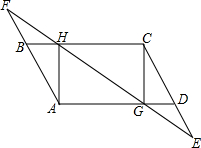 如图,分别延长平行四边形ABCD的边CD、AB到E、F,使DE=BF=$\frac{1}{2}$CD,连接EF,分别交AD,BC于G,H,连接CG,AH
如图,分别延长平行四边形ABCD的边CD、AB到E、F,使DE=BF=$\frac{1}{2}$CD,连接EF,分别交AD,BC于G,H,连接CG,AH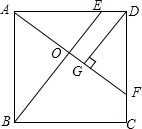 如图所示,正方形ABCD中,E、F分别是边AD、CD上的点,DE=CF,AF与BE相交于O,DG⊥AF,垂足为G.
如图所示,正方形ABCD中,E、F分别是边AD、CD上的点,DE=CF,AF与BE相交于O,DG⊥AF,垂足为G.