题目内容
17.为了提高产品的附加值,某公司计划将研发生产的1800件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多12天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的2倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
分析 设甲工厂每天能加工x件产品,表示出乙工厂每天加工2x件产品,然后根据甲加工产品的时间比乙加工产品的时间多10天列出方程求解即可.
解答 解:设甲工厂每天能加工x件产品,则乙工厂每天加工2x件产品,
根据题意得,$\frac{1800}{x}$-$\frac{1800}{2x}$=12,
解得x=75,
经检验,x=75是原方程的解,并且符合题意,
2x=2×75=150,
答:甲工厂每天能加工75件产品,乙工厂每天加工150件产品.
点评 此题考查了分式方程的应用,找出等量关系为两工厂的工作时间的差为12天是解题的关键.

练习册系列答案
相关题目
9.科学家发现一种病毒的直径约为0.0000403m,用科学记数法表示为( )
| A. | 4.03×105 | B. | 4.03×10-5 | C. | 4.03×10-6 | D. | 4.03×10-7 |
10.下列各式中是分式的是( )
| A. | 2x | B. | $\frac{1}{6}$(x-y) | C. | $\frac{x}{3}$ | D. | $\frac{1}{x+1}$ |
12.不等式组$\left\{\begin{array}{l}{2(x-3)>3x-7}\\{x-2>6-3x}\end{array}\right.$的解集是( )
| A. | x<1 | B. | x>2 | C. | 1<x<2 | D. | 无解 |
5.一次函数y=ax+b(a<0)图象上有A、B两点,A(x1,y1),B(x2,y2),且x1>x2,则y1和y2的大小关系为( )
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 无法判断 |
 (x>0)上一点,直线AB平行于y轴交直线y=x于点A,交x轴于点D,
(x>0)上一点,直线AB平行于y轴交直线y=x于点A,交x轴于点D, 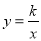 与直线y=x交于点C,若OB2﹣AB2=4
与直线y=x交于点C,若OB2﹣AB2=4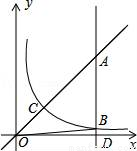
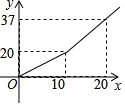 为鼓励节约用水,某市自来水公司对居民用水采用以户为单位分段计费办法收费,即一个月用水10t以内(包含10t)的用户,收水费a元/t,一月用水超过10t的用户,超出的部分按b元/t(b>a)收费,设一户居民用水x t,应收水费y元,y与x之间的函数关系式如图所示:按上述分段收费标准,小兰家3月份和4月份分别交水费29.1元和20.8元,则小兰家4月份比3月份节约用水4.9吨.
为鼓励节约用水,某市自来水公司对居民用水采用以户为单位分段计费办法收费,即一个月用水10t以内(包含10t)的用户,收水费a元/t,一月用水超过10t的用户,超出的部分按b元/t(b>a)收费,设一户居民用水x t,应收水费y元,y与x之间的函数关系式如图所示:按上述分段收费标准,小兰家3月份和4月份分别交水费29.1元和20.8元,则小兰家4月份比3月份节约用水4.9吨. 如图,在四边形ABCD中,对角线AC⊥BD,E、F分别是AB、CD的中点.若AC=4cm,BD=6cm,则EF=$\sqrt{13}$cm.
如图,在四边形ABCD中,对角线AC⊥BD,E、F分别是AB、CD的中点.若AC=4cm,BD=6cm,则EF=$\sqrt{13}$cm.