题目内容
8．已知$\frac{x}{y+z}$=$\frac{y}{z+x}$=$\frac{z}{x+y}$，求分式$\frac{x+y+z}{x}$的值．分析 已知等式利用合比性质求出值，原式变形后代入计算即可求出值．
解答 解：已知等式变形得：$\frac{x}{y+z}$=$\frac{y}{z+x}$=$\frac{z}{x+y}$=$\frac{x+y+z}{2（x+y+z）}$=$\frac{1}{2}$，
∴$\frac{y+z}{x}$=2，
则原式=1+2=3．
点评 此题考查了分式的值，熟练掌握比例的性质是解本题的关键．
练习册系列答案
相关题目
如图，CA⊥AB，CA=AB，DA=AE，BD=CE，求证：DA⊥EA．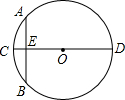
“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题，“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问锯几何？”用现代的数学语言表述是：“如图，CD为⊙O的直径，弦AB⊥CD垂足为E，CE=1寸，AB=10寸，求直径CD的长”，依题意，CD长为（ ）
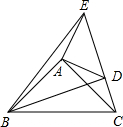已知：如图在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C，D，E三点在同一条直线上，连接BD，BE．以下四个结论：①BD=CE；②BD⊥CE；③∠ACE+∠DBC=45°；④BE2=2（AD2+AB2）-CD2，其中结论正确的个数是（ ）