题目内容
5. 如图所示,两块三角板的直角顶点O重叠在一起,且OB恰好平分∠COD,则∠AOD的度数为( )
如图所示,两块三角板的直角顶点O重叠在一起,且OB恰好平分∠COD,则∠AOD的度数为( )| A. | 100° | B. | 120° | C. | 135° | D. | 150° |
分析 本题是有公共定点的两个直角三角形问题,通过图形可知∠AOC+∠BOC=90°,∠BOD+∠BOC=90°,同时∠AOC+∠BOC+∠BOD+∠BOC=180°,可以通过角平分线性质求解.
解答 解:∵OB平分∠COD,
∴∠COB=∠BOD=45°,
∵∠AOB=90°,
∴∠AOC=45°,
∴∠AOD=135°.
故选:C.
点评 本题考查了角的平分线与对顶角的性质,角平分线的性质是将两个角分成相等的两个角.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
15. 如图,∠A=80°,点O是AB,AC垂直平分线的交点,则∠BCO的度数是( )
如图,∠A=80°,点O是AB,AC垂直平分线的交点,则∠BCO的度数是( )
 如图,∠A=80°,点O是AB,AC垂直平分线的交点,则∠BCO的度数是( )
如图,∠A=80°,点O是AB,AC垂直平分线的交点,则∠BCO的度数是( )| A. | 40° | B. | 30° | C. | 20° | D. | 10° |
16.如果x的相反数是2,那么x的值是( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
13. 若实数a,b在数轴上的位置如图所示,则化简|a+b|-|a-b|的结果是( )
若实数a,b在数轴上的位置如图所示,则化简|a+b|-|a-b|的结果是( )
 若实数a,b在数轴上的位置如图所示,则化简|a+b|-|a-b|的结果是( )
若实数a,b在数轴上的位置如图所示,则化简|a+b|-|a-b|的结果是( )| A. | -2b | B. | b | C. | -2a | D. | 2a-b |
20.下列图象不能表示y是x的函数图象的是( )
| A. |  | B. |  | C. |  | D. |  |
10. 下面是利用尺规作∠AOB的角平分线OC的作法:
下面是利用尺规作∠AOB的角平分线OC的作法:
①以点O为圆心,适当长为半径画弧,交OA、OB于点D,E;
②分别以点D,E为圆心,以大于$\frac{1}{2}$DE的长为半径作弧,两弧在∠AOB内部交于点C;
③画射线OC,射线OC就是∠AOB的平分线.
如图,在用尺规作角平分线过程中,用到的三角形全等的判定方法是( )
 下面是利用尺规作∠AOB的角平分线OC的作法:
下面是利用尺规作∠AOB的角平分线OC的作法:①以点O为圆心,适当长为半径画弧,交OA、OB于点D,E;
②分别以点D,E为圆心,以大于$\frac{1}{2}$DE的长为半径作弧,两弧在∠AOB内部交于点C;
③画射线OC,射线OC就是∠AOB的平分线.
如图,在用尺规作角平分线过程中,用到的三角形全等的判定方法是( )
| A. | ASA | B. | SAS | C. | SSS | D. | AAS |
14. 如图,点C、D在以AB为直径的⊙O上,且CD平分∠ACB,若AB=2,∠CBA=15°,则CD的长为( )
如图,点C、D在以AB为直径的⊙O上,且CD平分∠ACB,若AB=2,∠CBA=15°,则CD的长为( )
 如图,点C、D在以AB为直径的⊙O上,且CD平分∠ACB,若AB=2,∠CBA=15°,则CD的长为( )
如图,点C、D在以AB为直径的⊙O上,且CD平分∠ACB,若AB=2,∠CBA=15°,则CD的长为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{2}$ |
14. 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )| A. | 4 | B. | 6 | C. | 4$\sqrt{2}$ | D. | 4$\sqrt{3}$ |
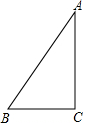 如图,在Rt△ABC中,∠C=90°,∠B=60°,将△ABC绕点A逆时针旋转60°,点B、C分别落在点B′、C′处,联结BC′与AC边交于点D,那么$\frac{BD}{DC′}$=$\frac{2}{3}$.
如图,在Rt△ABC中,∠C=90°,∠B=60°,将△ABC绕点A逆时针旋转60°,点B、C分别落在点B′、C′处,联结BC′与AC边交于点D,那么$\frac{BD}{DC′}$=$\frac{2}{3}$.