题目内容
14. 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )| A. | 4 | B. | 6 | C. | 4$\sqrt{2}$ | D. | 4$\sqrt{3}$ |
分析 根据AD是中线,得出CD=4,再根据AA证出△CBA∽△CAD,得出$\frac{AC}{BC}$=$\frac{CD}{AC}$,求出AC即可.
解答 解:∵BC=8,
∴CD=4,
在△CBA和△CAD中,
∵∠B=∠DAC,∠C=∠C,
∴△CBA∽△CAD,
∴$\frac{AC}{BC}$=$\frac{CD}{AC}$,
∴AC2=CD•BC=4×8=32,
∴AC=4$\sqrt{2}$;
故选C.
点评 此题考查了相似三角形的判断与性质,关键是证出△CBA∽△CAD,是一道基础题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
5. 如图所示,两块三角板的直角顶点O重叠在一起,且OB恰好平分∠COD,则∠AOD的度数为( )
如图所示,两块三角板的直角顶点O重叠在一起,且OB恰好平分∠COD,则∠AOD的度数为( )
 如图所示,两块三角板的直角顶点O重叠在一起,且OB恰好平分∠COD,则∠AOD的度数为( )
如图所示,两块三角板的直角顶点O重叠在一起,且OB恰好平分∠COD,则∠AOD的度数为( )| A. | 100° | B. | 120° | C. | 135° | D. | 150° |
4.单项式-$\frac{2abc}{3}$的系数和次数分别是( )
| A. | -$\frac{2}{3}$,3 | B. | -$\frac{2}{3}$,1 | C. | -2,3 | D. | -2,1 |
 如图,在△ABC中,AB=AC=10,BC=16,点D、E分别是BC、AC边上的点,且∠ADE=∠B,EA=DE,则BD的长=$\frac{39}{4}$.
如图,在△ABC中,AB=AC=10,BC=16,点D、E分别是BC、AC边上的点,且∠ADE=∠B,EA=DE,则BD的长=$\frac{39}{4}$.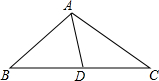 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为4$\sqrt{2}$.
如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为4$\sqrt{2}$. 如图,已知△ABC中,点D在边BC上,∠DAB=∠B,点E在边AC上,满足AE•CD=AD•CE.
如图,已知△ABC中,点D在边BC上,∠DAB=∠B,点E在边AC上,满足AE•CD=AD•CE.