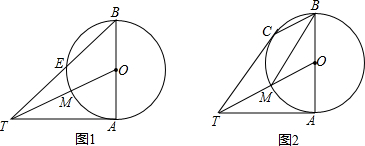题目内容
7.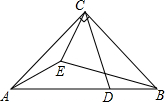 如图,在△ABC中,∠ACB=90°,AC=BC,点D在AB上,AD=9,BD=3,EA=EC,∠ECD=45°,则BE的长为$\frac{3\sqrt{26}}{2}$.
如图,在△ABC中,∠ACB=90°,AC=BC,点D在AB上,AD=9,BD=3,EA=EC,∠ECD=45°,则BE的长为$\frac{3\sqrt{26}}{2}$.
分析 延长CE交AB于M,作MN⊥AC于N,EK⊥AC于K,EF⊥BC于F,将△ACM绕点C逆时针旋转90°得到△CBH,连接DH,欲求BE只要求出EF、BF即可,首先证明DM2=AM2=DB2,利用这个关系可以求出AM,再根据勾股定理、平行线分线段成比例定理即可解决问题.
解答 解:延长CE交AB于M,作MN⊥AC于N,EK⊥AC于K,EF⊥BC于F,将△ACM绕点C逆时针旋转90°得到△CBH,连接DH.
∵∠ACM=∠BCE,∠MCD=45°,
∴∠ACM+∠BCD=45°,
∴∠BCD+∠BCH=45°,
∴∠DCM=∠DCH,
在△CDM和△CDH中,
$\left\{\begin{array}{l}{CD=CD}\\{∠DCM=∠DCH}\\{CM=CH}\end{array}\right.$,
∴△CDM≌△CDH,
∴MD=DH,
∵∠A=∠CBH=45°,∠ABC=45°,AM=BH,
∴∠DBH=90°,DH2=BH2+DB2,
∴DM2=AM2+BD2,设AM=x,则DM=9-x,(9-x)2=32+x2,解得x=4,
∴AM=4,DM=5,
∵△ABC,△AMN都是等腰直角三角形,
∴AC=BC=6$\sqrt{2}$,AN=MN=2$\sqrt{2}$,
∵EK⊥AC,EA=EC,
∴AK=KC=3$\sqrt{2}$,NK=AK-AN=$\sqrt{2}$,
∵EK∥MN,
∴$\frac{CK}{CN}=\frac{EK}{MN}$,
∴EK=$\frac{3\sqrt{2}}{2}$,
∵∠EKC=∠EFC=∠KCF=90°,
∴四边形KEFC是矩形,
∴KC=EF=3$\sqrt{2}$,KE=CF=$\frac{3\sqrt{2}}{2}$,
∴BF=BC-CF=$\frac{9\sqrt{2}}{2}$,
∴BE=$\sqrt{E{F}^{2}+B{F}^{2}}$=$\frac{3\sqrt{26}}{2}$.
故答案为$\frac{3\sqrt{26}}{2}$.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质、勾股定理等知识,解题的关键是利用旋转构造全等三角形,学会利用勾股定理解决线段问题,题目有点难度.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | a+2a2=3a3 | B. | (a3)2=a5 | C. | a3•a2=a6 | D. | a6÷a2=a4 |
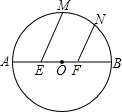 如图,已知⊙O的直径AB=12,E、F为AB的三等分点,M、N为$\widehat{AB}$上两点,且∠MEB=∠NFB=60°,则EM+FN=( )
如图,已知⊙O的直径AB=12,E、F为AB的三等分点,M、N为$\widehat{AB}$上两点,且∠MEB=∠NFB=60°,则EM+FN=( )| A. | $\frac{\sqrt{33}}{2}$ | B. | $\sqrt{33}$ | C. | 2$\sqrt{33}$ | D. | 33 |
| A. | y2>y1>y3 | B. | y1>y2>y3 | C. | y3>y1>y2 | D. | y3>y2>y1 |