题目内容
2.已知:如图1,在四边形ABCD中,AB∥CD,∠B=∠D.(1)求证:四边形ABCD是平行四边形;
(2)过点A作AE⊥BC于E,AF⊥CD于F,如图2,若CF=2,CE=5,四边形ABCD的周长为28.求EF的长度.
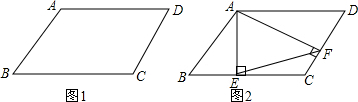
分析 (1)利用平行线的性质“两直线平行,同旁内角互补”和已知条件判定“同旁内角互补”,则两直线平行得到AD∥BC,于是得到结论;
(2)由四边形ABCD是平行四边形,得到∠B=∠D,由于∠AEB=∠AFD=90°,得到△ABE∽△ADF,得到$\frac{AB}{AD}$=$\frac{BE}{DF}$,根据比例的性质得到$\frac{AB+AD}{AD}$=$\frac{BE+DF}{DF}$,得到AD=2DF,根据直角三角形的性质得到∠DAF=30°,∠D=60°,求出∠C=120°,由余弦定理求得结果.
解答 (1)证明:∵在四边形ABCD中,AB∥CD,
∴∠A+∠D=180°.
又∠B=∠D,
∴∠A+∠B=180°,
∴AD∥BC,
∴四边形ABCD是平行四边形;
(2)解:设BC=x,CD=y,
∴x+y=14,
BE+DF=14-(5+2)=7,
∵四边形ABCD是平行四边形,
∴∠B=∠D,
∵∠AEB=∠AFD=90°,
∴△ABE∽△ADF,
∴$\frac{AB}{AD}$=$\frac{BE}{DF}$,
∴$\frac{AB+AD}{AD}$=$\frac{BE+DF}{DF}$,
∴$\frac{14}{AD}$=$\frac{7}{DF}$,
∴AD=2DF,
∴∠DAF=30°,∠D=60°,
∠C=120°,
根据余弦定理得:EF2=52+22-2×5×2•cos120°=25+4+10=39,
∴$EF=\sqrt{39}$.
点评 本题考查了平行四边形的性质和判定,相似三角形的判定和性质,余弦定理,知道根据余弦定理解决问题是解题的关键.

练习册系列答案
相关题目
14.已知图(1)、(2)中各有两个三角形,其边长和角的度数已在图上标注,图(2)中AB、CD交于O点,对于各图中的两个三角形而言,下列说法正确的是( )


| A. | 只有(1)相似 | B. | 只有(2)相似 | C. | 都相似 | D. | 都不相似 |
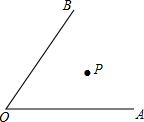 如图,某市的牛奶加工长P恰好在两条铁路OA、OB的夹角内部,为了提高牛奶的销量,经理决定在这两条铁路沿线上各建一个转运站M、N,加工厂的运货车每天从加工厂P向转运站M、N运送成品牛奶,问转运站M、N应建在何处,能够使运货车以最短的路程回到加工厂P?
如图,某市的牛奶加工长P恰好在两条铁路OA、OB的夹角内部,为了提高牛奶的销量,经理决定在这两条铁路沿线上各建一个转运站M、N,加工厂的运货车每天从加工厂P向转运站M、N运送成品牛奶,问转运站M、N应建在何处,能够使运货车以最短的路程回到加工厂P?
 已知如图,∠1=∠2,CF⊥AB、DE⊥AB,那么∠AFG和∠B是否相等,请说明理由.
已知如图,∠1=∠2,CF⊥AB、DE⊥AB,那么∠AFG和∠B是否相等,请说明理由.