题目内容
一个n边形的每个内角都等于140°，则n= ．
考点：多边形内角与外角
专题：
分析：根据多边形的内角和定理：180°•（n-2）求解即可．
解答：解：由题意可得：180°•（n-2）=140°•n，
解得n=9．
故答案为：9．
解得n=9．
故答案为：9．
点评：主要考查了多边形的内角和定理．n边形的内角和为：180°•（n-2）．此类题型直接根据内角和公式计算可得．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
小学学习好帮手系列答案
相关题目
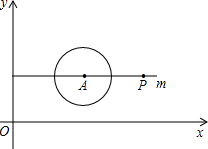如图，在平面直角坐标系中，O为坐标原点，点A的坐标为（4，3），⊙A的半径为2，过点A作直线m∥x轴，点P在直线m上运动．当点P在⊙A上时，求点P的坐标．若点P的横坐标为12，试猜想直线OP与⊙A的位置关系，并证明你的猜想．
如图中，若BD、CD为角平分线，且∠A=50°，∠E=130°，∠则∠D=
如图，点A为正比例函数y=kx的图象上一点，过A作AB⊥x于B，交正比例函数y=x的图象于点C，且S△AOC=S△BOC，求k的值．若
+1-4b+4b2=0，则a2+
+b的值为（ ）
| a2-4a+4 |
| 1 |
| a |
| A、4 | B、5.5 | C、4.5 | D、5 |
下列说法不正确的是（ ）
A、
| ||||
B、
| ||||
| C、（-0.1）2的算术平方根是0.1 | ||||
| D、8的立方根是±2 |
如图，在△ABC中，∠A、∠B的角平分线交于点O，过O作OP⊥BC于P，OQ⊥AC于Q，OR⊥AB于R，AB=7，BC=8，AC=9，则BP+CQ-AR=下列各组数中，互为相反数的是（ ）
A、2和
| ||
| B、-2和-|x| | ||
| C、-2和|-2| | ||
| D、-2和|y| |