如图.在△A1B1C1中.已知A1B1=5.B1C1=7.A1C1=4.依次连接△A1B1C1三边中点.得△A2B2C2.再依次连接△A2B2C2的三边中点得△A3B3C3.-.则△A5B5C5的周长=1．题目和参考答案——青夏教育精英家教网—

题目内容

19．

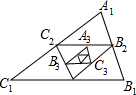如图，在△A₁B₁C₁中，已知A₁B₁=5，B₁C₁=7，A₁C₁=4，依次连接△A₁B₁C₁三边中点，得△A₂B₂C₂，再依次连接△A₂B₂C₂的三边中点得△A₃B₃C₃，…，则△A₅B₅C₅的周长=1．

分析由三角形的中位线定理得：A₂B₂、B₂C₂、C₂A₂分别等于A₁B₁、B₁C₁、C₁A₁的一半，所以△A₂B₂C₂的周长等于△A₁B₁C₁的周长的一半，以此类推可求出△A₅B₅C₅的周长为△A₁B₁C₁的周长关系，问题得解．

解答解：∵A₂B₂、B₂C₂、C₂A₂分别等于A₁B₁、B₁C₁、C₁A₁的一半，
∴以此类推：△A₅B₅C₅的周长为△A₁B₁C₁的周长的$\frac{1}{{2}^{4}}$=$\frac{1}{16}$，
∴则△A₅B₅C₅的周长为（7+4+5）÷16=1．
故答案为：1．

点评本题主要考查了三角形的中位线定理，关键是根据三角形的中位线定理得：A₂B₂、B₂C₂、C₂A₂分别等于A₁B₁、B₁C₁、C₁A₁的一半，所以△A₂B₂C₂的周长等于△A₁B₁C₁的周长的一半．

练习册系列答案

相关题目

9．以下列各线段为边，能组成直角三角形的是（　　）

	A．	两条对角线互相垂直平分的四边形是菱形
	B．	两条对角线相等且互相垂直的四边形是矩形
	C．	有两个角相等的梯形是等腰梯形
	D．	两条对角线平分且相等的四边形是正方形

7．已知2+$\frac{2}{3}$=2²×$\frac{2}{3}$，3+$\frac{3}{8}$=3²×$\frac{3}{8}$，4+$\frac{4}{15}$=4²×$\frac{4}{15}$，…，且10+$\frac{a}{b}$=10²×$\frac{a}{b}$（a，b均为正整数）．
（1）探究a，b的值；
（2）求分式$\frac{{a}^{2}+4ab+4{b}^{2}}{{a}^{2}+2ab}$的值．

14．

作图题
在如图的方格纸中，每个小方格都是边长为1个单位的正方形，△ABC的三个顶点都在格点上（每个小方格的顶点叫格点）
（1）作△ABC关于点P的中心对称图形△A₁B₁C₁；
（2）设P（0，0），C（-1，0），作△ABC绕点B沿顺时针方向旋转90°而得到的△A₂B₂C₂；并写出此时A的坐标．

4．已知：在Rt△ABC中，∠C=90°，AC=6，BC=8，点E是边AC上一动点，过点E作EF∥BC，交AB边于点F，点D为BC上任一点，连接DE、DF，设EC长为x，则△DEF面积y关于x的函数图象大致为（　　）

11．

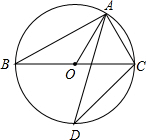如图，A、D是⊙O上的两点，BC是直径，若∠D=35°，则∠OCA的度数是（　　）

8．已知$\frac{n}{m}$=2，则$\frac{n}{n-m}$-$\frac{m}{n+m}$=1$\frac{2}{3}$．

9．如图，圆弧形石拱桥的桥顶到水面的距离CD为6m，桥拱半径OC为4m，则水面宽AB为（　　）

试题分类