题目内容
7.已知关于x的方程x2-2(m+1)x+m2=0(1)当m取何值时,方程有两个实数根:
(2)为m选取一个合适的整数,使方程有两个不相等的实数根,并求出这两个根,你选取的m的值为0.
分析 (1)方程有两个实数根,必须满足△=b2-4ac≥0,从而建立关于m的不等式,求出实数m的取值范围.
(2)答案不唯一,方程有两个不相等的实数根,即△>0,可以解得m>-$\frac{1}{2}$,在m>-$\frac{1}{2}$的范围内选取一个合适的整数求解就可以.
解答 解:(1)由题意知:△=b2-4ac=[-2(m+1)]2-4m2=[-2(m+1)+2m][-2(m+1)-2m]=-2(-4m-2)=8m+4≥0,
解得m≥-$\frac{1}{2}$.
∴当m≥-$\frac{1}{2}$时,方程有两个实数根.
(2)选取m=0.(答案不唯一,注意开放性)
方程为x2-2x=0,
解得x1=0,x2=2.
故答案为:0.
点评 此题主要考查了根的判别式,以及解一元二次方程,关键是掌握一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
18.若三元一次方程组$\left\{\begin{array}{l}{x+y=5}\\{x+z=-1}\\{y+z=-2}\end{array}\right.$的解使ax+2y+z=0,则a的值为( )
| A. | 1 | B. | 0 | C. | -2 | D. | 4 |
17.下列命题中,是真命题的是( )
| A. | 如果∠1+∠2=180°,那么∠1与∠2互为邻补角 | |
| B. | 相等的角是对顶角 | |
| C. | 两条直线被第三条直线所截,同旁内角互补 | |
| D. | 在同一平面内,垂直于同一直线的两条直线平行 |
 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D.求AD的长.
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D.求AD的长.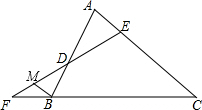 已知,如图,在△ABC中,∠A=∠ABC,直线EF分别交△ABC的边AB,AC和CB的延长线于点D,E,F.
已知,如图,在△ABC中,∠A=∠ABC,直线EF分别交△ABC的边AB,AC和CB的延长线于点D,E,F.