题目内容
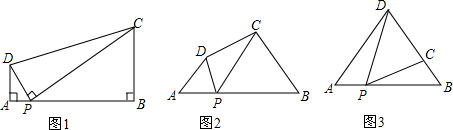
19．
如图所示，D是△ABC的边BC上的一点，且∠1=∠2，∠3=∠4，∠BAC=63°，则∠DAC=24°．
分析 根据三角形外角的性质可得∠3=∠1+∠2，结合条件可得∠4=2∠2，然后在△ABC中运用三角形内角和定理可求出∠2，即可得到∠1，从而可求出∠DAC．
解答 解：∵∠3=∠1+∠2，∠1=∠2，∠3=∠4，
∴∠4=2∠2．
∵∠2+∠4+∠BAC=180°，∠BAC=63°，
∴3∠2+63°=180°，
∴∠2=39°，
∴∠1=∠2=39°，
∴∠DAC=63°-39°=24°．
故答案为24°．
点评 本题主要考查了三角形内角和定理、三角形外角的性质等知识，得到∠4与∠2的关系是解决本题的关键．
练习册系列答案
教材全解字词句篇系列答案
相关题目
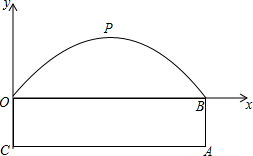如图所示，某隧道横截面的轮廓线由抛物线对称的一部分和矩形的一部分组成，最大高度为6米，底部宽度为12米，OC=3米，现如图建立平面直角坐标系．
7．已知a是有理数，下列各式：（-a）2=a2；-a2=（-a）2；（-a）3=a3；|-a3|=a3．其中一定成立的有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
