题目内容
19.计算:(1)$\frac{2a}{a+1}$+$\frac{2}{a+1}$;
(2)(y+2)2-(y-1)(y+5).
分析 (1)利用同分母的分式的加法法则,分母不变,分子相加,然后进行化简即可;
(2)首先利用完全平方公式以及多项式的乘法法则计算,然后去括号、合并同类项即可求解.
解答 解:(1)原式=$\frac{2a+2}{a+1}$
=$\frac{2(a+1)}{a+1}$
=2;
(2)原式=y2+4y+4-(y2+4y-5)
=y2+4y+4-y2-4y+5
=9.
点评 本题考查了分式的加法以及整式的混合运算,正确理解完全平方公式以及多项式的乘法法则是关键.

练习册系列答案
相关题目
9.函数y=kx与y=-$\frac{k}{x}$在同一坐标系内的大致图象是( )
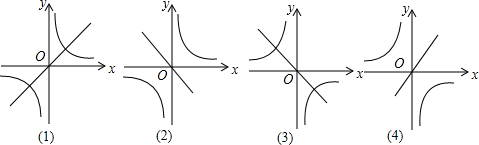

| A. | (1)和(2) | B. | (1)和(3) | C. | (2)和(3) | D. | (2)和(4) |
7.下列说法正确的是( )
| A. | 三角形的中线就是过顶点平分对边的直线 | |
| B. | 三角形的三条角平分线的交点有可能在三角形外部 | |
| C. | 三角形的三条高线的交点必在三角形内部 | |
| D. | 以上说法都错 |
14.下列运算中,正确的是( )
| A. | (-a2b3)2=a4b6 | B. | (-2a)2=-4a2 | C. | (a+b)2=a2+b2 | D. | b2•b3=2b3 |
4.在二次函数y=(x-1)2-1中,常数项是( )
| A. | 1 | B. | -1 | C. | 0 | D. | -2 |
11.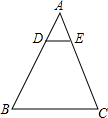 如图,在△ABC中,DE∥BC,$\frac{AD}{DB}=\frac{1}{2}$,DE=4,则BC的长( )
如图,在△ABC中,DE∥BC,$\frac{AD}{DB}=\frac{1}{2}$,DE=4,则BC的长( )
 如图,在△ABC中,DE∥BC,$\frac{AD}{DB}=\frac{1}{2}$,DE=4,则BC的长( )
如图,在△ABC中,DE∥BC,$\frac{AD}{DB}=\frac{1}{2}$,DE=4,则BC的长( )| A. | 8 | B. | 10 | C. | 12 | D. | 16 |
8.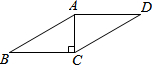 如图,在?ABCD中,过A点作高,垂足刚好为点C,AC=2,∠B=30°,则?ABCD的周长是( )
如图,在?ABCD中,过A点作高,垂足刚好为点C,AC=2,∠B=30°,则?ABCD的周长是( )
 如图,在?ABCD中,过A点作高,垂足刚好为点C,AC=2,∠B=30°,则?ABCD的周长是( )
如图,在?ABCD中,过A点作高,垂足刚好为点C,AC=2,∠B=30°,则?ABCD的周长是( )| A. | $8+4\sqrt{3}$ | B. | $4+2\sqrt{3}$ | C. | 8 | D. | 4 |
 如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是45cm2,AB=16cm,AC=14cm,则DE=3.
如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是45cm2,AB=16cm,AC=14cm,则DE=3.