题目内容
9. 我们知道,求圆环的面积可以转化为求大圆与小圆面积的差.
我们知道,求圆环的面积可以转化为求大圆与小圆面积的差.(1)如图①,直线l与小圆相切于点P,与大圆相交于点A,B.
①求证:AP=BP;
②若AB=10,求圆环的面积;
(2)如图②,直线l与大圆、小圆分别交于点A,B,C,D,若AB=10,AC=2,则圆环的面积为16π.
分析 (1)①连结OP,如图①,先根据切线的性质得OP⊥AB,然后根据垂径定理即可得到AP=BP;
②连结OA,如图①,AP=BP=$\frac{1}{2}$AB=5,根据勾股定理得到OA2-OP2=AP2=25,然后根据圆的面积公式,利用圆环的面积=S大圆-S小圆进行计算;
(2)作OE⊥CD于E,如图②,根据垂径定理得到AE=BE=$\frac{1}{2}$AB=5,则CE=AE-AC=3,再利用勾股定理得OA2=OE2+AE2,OC2=OE2+CE2,然后根据圆的面积公式,利用圆环的面积=S大圆-S小圆进行计算.
解答 (1)①证明:连结OP,如图①,
∵直线l与小圆相切于点P,
∴OP⊥AB,
∴AP=BP;
②解:连结OA,如图①,AP=BP=$\frac{1}{2}$AB=5,
在Rt△OPA中,OA2-OP2=AP2=25,
∴圆环的面积=S大圆-S小圆=π•OA2-π•OP2=π(OA2-OP2)=25π;
(2)解:作OE⊥CD于E,如图②,
∵AB=10,AC=2,
∴AE=$\frac{1}{2}$AB=5,
∴CE=AE-AC=5-2=3,
∵OA2=OE2+AE2,OC2=OE2+CE2,
∴圆环的面积=S大圆-S小圆=π•OA2-π•OC2=π(AE2-CE2)=(25-9)π=16π.
故答案为16π.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了垂径定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.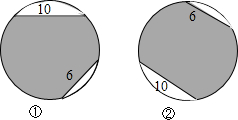 在图①、图②中的两个等圆中,各有两条长分别为10和6的弦,两图阴影面积S的大小关系为( )
在图①、图②中的两个等圆中,各有两条长分别为10和6的弦,两图阴影面积S的大小关系为( )
 在图①、图②中的两个等圆中,各有两条长分别为10和6的弦,两图阴影面积S的大小关系为( )
在图①、图②中的两个等圆中,各有两条长分别为10和6的弦,两图阴影面积S的大小关系为( )| A. | S①>S② | B. | S①<S② | C. | S①=S② | D. | 无法确定 |
4.某校篮球队9名主力队员中有4人调到省队学习训练,学校又从其它省市重新物色了4名球员加入主力队伍,新老队员的身体素质和技战术水平的综合能力得分如表所示:
球队调整后与调整前相比,综合能力得分的方差变小(填“变小”、“不变”或“变大”).
| 编号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ |
| 原来球队 | 72 | 72 | 77 | 77 | 78 | 80 | 86 | 86 | 92 |
| 现在球队 | 72 | 72 | 77 | 77 | 78 | 93 | 84 | 83 | 84 |
1.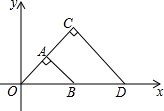 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:4,∠OCD=90°,CO=CD.若点B的坐标为(1,0),则点C的坐标为( )
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:4,∠OCD=90°,CO=CD.若点B的坐标为(1,0),则点C的坐标为( )
 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:4,∠OCD=90°,CO=CD.若点B的坐标为(1,0),则点C的坐标为( )
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:4,∠OCD=90°,CO=CD.若点B的坐标为(1,0),则点C的坐标为( )| A. | (2,2) | B. | (2,4) | C. | (2$\sqrt{2},2\sqrt{2}$) | D. | (4,2) |
 如图所示,BE=FC=$\frac{1}{3}$BC,D是AE的中点,△DEF的面积是5平方厘米,求△ABC的面积.
如图所示,BE=FC=$\frac{1}{3}$BC,D是AE的中点,△DEF的面积是5平方厘米,求△ABC的面积.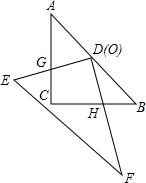 如图:一幅三角板如图放置,等腰直角△ABC固定不动,另一块△DEF的直角顶点放在等腰直角△ABC的斜边AB中点O 处,且可以绕点O旋转,在旋转过程中,两直角边的交点G、H始终在边AC、BC上.
如图:一幅三角板如图放置,等腰直角△ABC固定不动,另一块△DEF的直角顶点放在等腰直角△ABC的斜边AB中点O 处,且可以绕点O旋转,在旋转过程中,两直角边的交点G、H始终在边AC、BC上.