题目内容
(1)如图1,正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长
CD到点G,使DG=BE,连结EF,AG.求证:EF=FG.
(2)如图2,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边
BC上,且∠MAN=45°,若BM=1,CN=3,求MN的长.
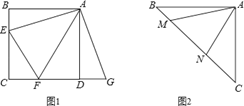

(1)证明:∵ABCD为正方形,
∴∠ABE=∠ADG,AD=AB,
在△ABE和△ADG中,
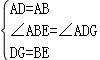
∴△ABE≌△ADG(SAS), 3分
∴∠BAE=∠DAG,AE =AG,
=AG,
∴∠EAG=90°,
在△FAE和△GAF中,
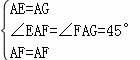 ,
,
∴△FAE≌△GAF(SAS),
∴EF=FG 6分
(2)解:如图2,过点C作CE⊥BC,垂足为点C,截取CE,使CE=BM.
连接AE、EN.

∵AB=AC,∠BAC=90°,∴∠B=∠ACN=45°.
∵CE⊥BC,∴∠ACE=∠B=45°.
在△ABM和△ACE中,
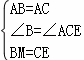
∴△ABM≌△ACE(SAS). 8分
∴AM=AE,∠BAM=∠CAE.
∵∠BAC=90°,∠MAN=45°,∴∠BAM+∠CAN=45°.
于是,由 ∠BAM=∠CAE,得∠MAN=∠EAN=45°.
∠BAM=∠CAE,得∠MAN=∠EAN=45°.
在△MAN和△EAN中,
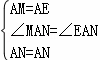
∴△MAN≌△EAN(SAS). 10分
∴MN=EN.
在Rt△ENC中,由勾股定理,得EN2=EC2+NC2.
∴MN2=BM2+NC2.
∵BM=1,CN=3,
∴MN2=12+32,
∴MN=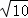 12分
12分

 的图象上有两点(-1,y1),(
的图象上有两点(-1,y1),( ,y2),则y1-y2的值是( )
,y2),则y1-y2的值是( ) ,求图中阴影部分的面积.
,求图中阴影部分的面积. 
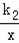 (k2为常数,且k2≠0)的图象都经过点A(2,3).则当x>2时,
(k2为常数,且k2≠0)的图象都经过点A(2,3).则当x>2时,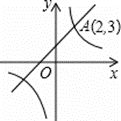
 的解是( )
的解是( ) 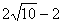 B、6 C、
B、6 C、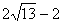 D、4
D、4
 可变形为
可变形为 B.
B.  C.
C.  D.
D. 