题目内容
7.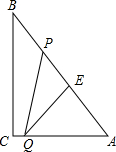 如图,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.点P从B出发沿BA 向A运动,速度为每秒1cm,点E是点B以P为对称中心的对称点.点P运动的同时,点Q从A出发沿AC向C运动,速度为每秒2cm.当点Q到达顶点C时,P,Q同时停止运动.设P,Q两点运动时间为t秒.
如图,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.点P从B出发沿BA 向A运动,速度为每秒1cm,点E是点B以P为对称中心的对称点.点P运动的同时,点Q从A出发沿AC向C运动,速度为每秒2cm.当点Q到达顶点C时,P,Q同时停止运动.设P,Q两点运动时间为t秒.(1)当x为何值时,PQ∥BC?
(2)设四边形PQCB的面积为y,求y关于t的函数解析式;
(3)四边形PQCB的面积与△APQ面积比为3:2?若能,求出此时t的值;若不能,请说明理由;
(4)当x为何值时,△AEQ为等腰三角形?
分析 (1)由勾股定理求出AB,由题意得出BP=EP=t,AQ=2t,则AP=10-t,CQ=6-2t,由平行线得出比例式,即可求出t的值;
(2)作PF⊥AQ于F,则PF∥BC,得出比例式求出PF,四边形PQCB的面积y=△ABC的面积-△APQ的面积,即可得出结果;
(3)分三种情况讨论:①当AE=AQ时;②当AE=QE时;③当AQ=EQ时;分别得出关于t的方程,解方程即可.
解答 解:(1)∵∠C=90°,
∴AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10,
根据题意得:BP=EP=t,AQ=2t,
则AP=10-t,CQ=6-2t,
当PQ∥BC时,△APQ∽△ABC,
∴$\frac{AQ}{AC}=\frac{AP}{AB}$=$\frac{PQ}{BC}$,
即$\frac{2t}{6}=\frac{10-t}{10}$,
解得:t=$\frac{30}{13}$;
∴当t=$\frac{30}{13}$时,PQ∥BC;
(2)作PF⊥AQ于F,如图1所示: 则PF∥BC,
则PF∥BC,
∴$\frac{PF}{BC}=\frac{AP}{AB}$,
即$\frac{PF}{8}=\frac{10-t}{10}$,
∴PF=8-$\frac{4}{5}$t,
∴四边形PQCB的面积y=△ABC的面积-△APQ的面积
=$\frac{1}{2}$×6×8-$\frac{1}{2}$×2t×(8-$\frac{4}{5}$t)=$\frac{4}{5}$t2-8t+24,
即y=$\frac{4}{5}$t2-8t+24;
(3)能;
根据题意得:$\frac{4}{5}$t2-8t+24=$\frac{3}{2}$×2t×(8-$\frac{4}{5}$t),
解得:t=5±$\sqrt{13}$,
∵6÷2=3,
∴0≤t≤3,
∴t=5-$\sqrt{13}$;
(4)分三种情况讨论:
①当AE=AQ时,10-2t=2t,
解得:t=$\frac{5}{2}$;
②当AE=QE时,点E在AQ的垂直平分线上,
则AE=EP,
∴10-2t=t,
解得:t=$\frac{10}{3}$,不合题意,舍去;
③当AQ=EQ时,
作EF⊥AQ于F,如图2所示:
则EF=8-$\frac{8}{5}$t,AF=6-$\frac{6}{5}$t,
∴QF=$\frac{16}{5}$t-6,
根据勾股定理得:(2t)2=(8-$\frac{8}{5}$t)2+($\frac{16}{5}$t-6)2,
解得:t=$\frac{25}{11}$,或t=5(不合题意,舍去),
∴t=$\frac{25}{11}$;
综上所述:当t=$\frac{5}{2}$或$\frac{25}{11}$时,△AEQ为等腰三角形.
点评 本题是相似形综合题目,考查了勾股定理、相似三角形的判定与性质、三角形面积的计算、等腰三角形的判定与性质等知识;本题难度较大,综合性强,特别是(3)中,需要进行分类讨论,根据题意得出方程才能得出结果.

| A. | ax2+bx+c=0 | B. | 2x2+3x=2x(x-1) | C. | (k2+1)x2-2x=6 | D. | x2-$\frac{5}{x}$+1=0 |
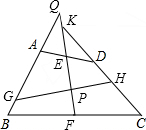 如图,四边形ABCD中,AB=CD,点E,F分别是AD,BC的中点,GH⊥EF交于点P.延长BA,FE相交于点Q,延长CD交FE的延长线于点K,求证:∠AGH=∠DHG.
如图,四边形ABCD中,AB=CD,点E,F分别是AD,BC的中点,GH⊥EF交于点P.延长BA,FE相交于点Q,延长CD交FE的延长线于点K,求证:∠AGH=∠DHG.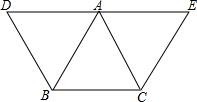 如图所示,已知BD∥AC,CE∥BA,且点D、A、E在一条直线上,设∠BAC=x,∠D+∠E=y.
如图所示,已知BD∥AC,CE∥BA,且点D、A、E在一条直线上,设∠BAC=x,∠D+∠E=y.