题目内容
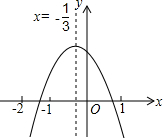 如图是二次函数y=ax2+bx+c(a≠0)的图象,有以下结论:
如图是二次函数y=ax2+bx+c(a≠0)的图象,有以下结论:①ab>0;②a+b+c<0;③b+2c<0;④a-2b+4c>0;⑤a=
| 3 |
| 2 |
其中正确的有
考点:二次函数图象与系数的关系
专题:数形结合
分析:由抛物线开口方向得a<0,由抛物线的对称轴得到b=
a<0,则可对①进行判断;由x=1时函数值为负数,可对②进行判断;由b=
a,得到a=
b,则可对⑤进行判断;由x=-1时,a-b+c>0,和a=
b得到b+2c>0,则可对③进行判断;由x=-
时,y>0,可对④进行判断.
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
解答:解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=-
=-
,
∴b=
a<0,
∴ac>0,所以①正确;
∵x=1时,y<0,
∴a+b+c<0,所以②正确;
∵b=
a,
∴a=
b,所以⑤正确;
而a=-1时,y>0,即a-b+c>0,
∴
b-b+c>0,
∴b+2c>0,所以③错误;
∵x=-
时,y>0,
∴
a-
b+c>0,
∴a-2b+4c>0,所以④正确.
故答案为①②④⑤.
∴a<0,
∵抛物线的对称轴为直线x=-
| b |
| 2a |
| 1 |
| 3 |
∴b=
| 2 |
| 3 |
∴ac>0,所以①正确;
∵x=1时,y<0,
∴a+b+c<0,所以②正确;
∵b=
| 2 |
| 3 |
∴a=
| 3 |
| 2 |
而a=-1时,y>0,即a-b+c>0,
∴
| 3 |
| 2 |
∴b+2c>0,所以③错误;
∵x=-
| 1 |
| 2 |
∴
| 1 |
| 4 |
| 1 |
| 2 |
∴a-2b+4c>0,所以④正确.
故答案为①②④⑤.
点评:本题考查了二次函数与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c).抛物线与x轴交点个数由△决定:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
御河中学校团委会要组织一次初三学生篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排78场比赛,则参赛球队的个数是( )
| A、11个 | B、12个 |
| C、13个 | D、14个 |
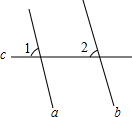 如图,a∥b,a、b被c所截,得到∠1=∠2的依据是( )
如图,a∥b,a、b被c所截,得到∠1=∠2的依据是( )| A、两直线平行,同位角相等 |
| B、两直线平行,内错角相等 |
| C、同位角相等,两直线平行 |
| D、内错角相等,两直线平行 |
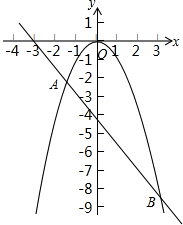 如图所示,抛物线y1=-x2与直线y2=-
如图所示,抛物线y1=-x2与直线y2=-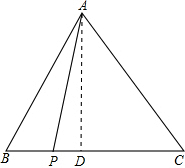 如图,在△ABC中,AB=AC=1,BC边上有2011个不同的点P1,P2,…,P2011,记mi=APi2+BPi•PiC(i=1,2,…,2011),则m1+m2+…+m2011=
如图,在△ABC中,AB=AC=1,BC边上有2011个不同的点P1,P2,…,P2011,记mi=APi2+BPi•PiC(i=1,2,…,2011),则m1+m2+…+m2011=