题目内容
若二次函数y=x2-mx的图象的顶点在直线y=x上,则m的值为 .
考点:二次函数的性质
专题:计算题
分析:先把解析式配成顶点式得到抛物线的顶点坐标为(
m,-
m2),再根据题意得到
m=-
m2,然后解关于m的一元二次方程即可.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
解答:解:∵y=(x-
m)2-
m2,
∴抛物线的顶点坐标为(
m,-
m2),
∵二次函数y=x2-mx的图象的顶点在直线y=x上,
∴
m=-
m2,
∴m=0或m=-2.
故答案为0或-2.
| 1 |
| 2 |
| 1 |
| 4 |
∴抛物线的顶点坐标为(
| 1 |
| 2 |
| 1 |
| 4 |
∵二次函数y=x2-mx的图象的顶点在直线y=x上,
∴
| 1 |
| 2 |
| 1 |
| 4 |
∴m=0或m=-2.
故答案为0或-2.
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
相关题目
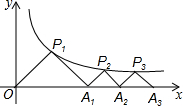 如图所示,P1(x1,y1)、P2(x2,y2),…,Pn(xn,yn)在函数y=
如图所示,P1(x1,y1)、P2(x2,y2),…,Pn(xn,yn)在函数y=