题目内容
14.在一个布口袋里装有红色、黑色、蓝色和白色的小球各1个,如果闭上眼睛随机地从布袋中取出一个球,记下颜色,放回布袋搅匀,再闭上眼睛随机的再从布袋中取出一个球.用树状图或列表法解决求:(1)连续两次恰好都取出白色球的概率;
(2)连续两次恰好取出一红、一黑的概率.
分析 (1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与连续两次恰好都取出白色球的情况,再利用概率公式即可求得答案;
(2)由(1)中的树状图,可求得连续两次恰好取出一红、一黑的情况,再利用概率公式即可求得答案.
解答 解:(1)画树状图得:
∵共有16种等可能的结果,连续两次恰好都取出白色球的只有1种情况,
∴连续两次恰好都取出白色球的概率为:$\frac{1}{16}$;
(2)∵连续两次恰好取出一红、一黑的有2种情况,
∴连续两次恰好取出一红、一黑的概率为:$\frac{2}{16}$=$\frac{1}{8}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.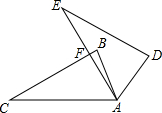 如图,△ABC中,∠C=30°,将△ABC绕点A顺时针旋转60°得△ADE,AE与BC交于F,则∠AFB为多少度?( )
如图,△ABC中,∠C=30°,将△ABC绕点A顺时针旋转60°得△ADE,AE与BC交于F,则∠AFB为多少度?( )
 如图,△ABC中,∠C=30°,将△ABC绕点A顺时针旋转60°得△ADE,AE与BC交于F,则∠AFB为多少度?( )
如图,△ABC中,∠C=30°,将△ABC绕点A顺时针旋转60°得△ADE,AE与BC交于F,则∠AFB为多少度?( )| A. | 70° | B. | 90° | C. | 60° | D. | 55° |
5.定义一种新运算“”,规定a※b=(a+2)×2-b,例如:3※5=(3+2)×2-5=5,根据上面的规定解答下面的问题:
(1)计算7※(-3);
(2)7※(-3)与(-7)※3相等吗?请说明理由.
(1)计算7※(-3);
(2)7※(-3)与(-7)※3相等吗?请说明理由.
2.已知点M(2,1)和点N(1,-2)在直线l:y=kx+b上,则直线l与x轴的交点坐标是( )
| A. | (0,-5) | B. | (-5,0) | C. | (0,$\frac{5}{3}$) | D. | ($\frac{5}{3}$,0) |
9.下列各组线段,能成比例的是( )
| A. | 3,6,9,18 | B. | 2,5,6,8 | C. | 1,2,3,4 | D. | 3,6,7,9 |