题目内容
已知:抛物线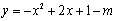 与x轴相交于A、B两点,与y轴相交于点C,其中
与x轴相交于A、B两点,与y轴相交于点C,其中
点C的坐标是(0,3),顶点为点D,联结CD,抛物线的对称轴与x轴交于点E.
(1)求m的值;
(2)求∠CDE的度数;
(3)在抛物线对称轴的右侧部分上是否存在一点P,使得△PDC是等腰三角形?如果
存在,求出符合条件的点P的坐标;如果不存在,请说明理由.
(1)∵抛物线过点C(0,3)
∴1-m=3
∴m=-2
(2)由(1)可知该抛物线的解析式为y=-x2+ 2x+3=-(x-1)2+4
2x+3=-(x-1)2+4
∴此抛物线的对称轴x=1
抛物线的顶 点D(1,4)
点D(1,4)
过点C作CF⊥DE,则CF∥OE
∴F(1,3)
所以CF=1,DF=4-3=1
∴CF=DF
又∵CF⊥DE
∴∠DFC=90°
∴∠CDE=45°
(3)存在.
①延长CF交抛物线于点P1,则CP1∥x轴,所以P1正好是C点关于DE的对称点时,有DC=DP1,得出P1点坐标(2,3);
由y=-x2+2x+3得,D点坐标为(1,4),对称轴为x=1.
②若以CD为底边,则PD=PC,
设P点坐标为(x,y),根据两点间距离公式,
得x2+(3-y)2=(x-1)2+(4-y)2,
即y=4-x.
又P点(x,y)在抛物线上,
∴4-x=-x2+2x+3,
即x2-3x+1=0,
解得:
 <1,应舍去;
<1,应舍去;
∴
∴y=4-x=
则P2点坐标( )
)
∴符合条件的点P坐标为( )和(2,3).
)和(2,3).

利用表格中的数据,可求出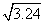 +(4.123)2-
+(4.123)2-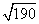 的近似值是(结果保留整数).
的近似值是(结果保留整数).
| A.3 | B.4 |
| C.5 | D.6 |
| a | a2 |
|
|
| 17 | 289 | 4.123 | 13.038 |
| 18 | 324 | 4.243 | 13.416 |
| 19 | 361 | 4.359 | 13.784 |

 小时.求自驾车平均速度和自行车平均速度各是多少.
小时.求自驾车平均速度和自行车平均速度各是多少. 如图,
如图, ,
, 与
与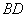 相交于点
相交于点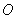 ,
, , 若
, 若 ,则
,则 等于_____.
等于_____.
