题目内容
2．
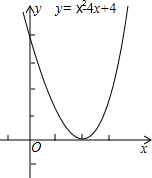（1）抛物线与x轴有1个交点，它们的横坐标是2；（2）当x取交点的横坐标时，函数值是0；
（3）所以方程x2+x-2=0的根是x1=-2，x2=1．
分析 （1）观察函数图象可判断抛物线与x轴只有一个交点，且交点的横坐标为2；
（2）利用x轴上点的坐标特征进行判断；
（3）方程x2+x-2=0的根就是抛物线y=x2+x-2与x轴交点的横坐标．
解答 解：（1）抛物线与x轴有1个交点，它的横坐标是2；
（2）当x取交点的横坐标时，函数值是0；
（3）方程x2+x-2=0的根是x1=-2，x2=1．
故答案为1，2；0；x1=-2，x2=1．
点评 本题考查了抛物线与x轴的交点：把求二次函数y=ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标问题转化为解关于x的一元二次方程．
练习册系列答案
相关题目
15．以下列数组作为三角形的三条边长，其中能构成直角三角形的是（ ）
| A． | 1，$\sqrt{2}$，3 | B． | $\sqrt{2}$，$\sqrt{3}$，5 | C． | 1.5，2，2.5 | D． | $\frac{1}{3}$，$\frac{1}{4}$，$\frac{1}{5}$ |
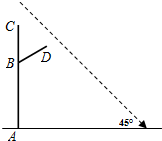如图，铜亭广场装有智能路灯，路灯设备由灯柱AC与支架BD共同组成（点C处装有安全监控，点D处装有照明灯），灯柱AC为6米，支架BD为2米，支点B到A的距离为4米，AC与地面垂直，∠CBD=60°．某一时刻，太阳光与地面的夹角为45°，求此刻路灯设备在地面上的影长为多少？
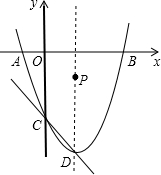如图，抛物线y=x2-2x-3与x轴交于A、B两点，与y轴交于点C，抛物线的顶点为D，问：在抛物线的对称轴上是否存在一点P，使得以P为圆心的圆经过A、B两点，并且与直线CD相切？若存在，求出点P 的坐标；若不存在，说明理由．