题目内容
17. 如图,已知△ABC中AB=AC,BD、CD分别平分∠EBA、∠ECA,BD交AC于F,连接AD.
如图,已知△ABC中AB=AC,BD、CD分别平分∠EBA、∠ECA,BD交AC于F,连接AD.(1)当∠BAC=50°时,求∠BDC的度数;
(2)请直接写出∠BAC与∠BDC的数量关系;
(3)求证:AD∥BE.
分析 (1)由外角关系∠BDC+$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠ACE,∠BAC+∠ABC=∠ACE,即可得出∠BDC=$\frac{1}{2}$∠BAC;
(2)由(1)的结论即可得到结果;
(3)作DM⊥BG于M,DN⊥AC于N,DH⊥BE于H根据角平分线的性质得到DM=DH,DN=DH,等量代换得到DM=DN,根据三角形的内角和得到∠GAD+∠CAD+∠BAC=180°,∠BAC+∠ABC+∠ACB=180°,推出∠GAD+∠CAD=∠ABC+∠ACB,由等腰三角形的性质得到∠ABC=∠ACB,等量代换得到∠GAD=∠ABC,推出AD∥BC.
解答 解:(1)∵AB=AC,∠BAC=50°,
∴∠ACB=∠ABC=65°,
∴∠ACE=115°,
∵BD、CD分别平分∠EBA、∠ECA,
∴∠DBC=$\frac{1}{2}$∠ABC=32.5°,∠DCE=$\frac{1}{2}$∠ACE=57.5°,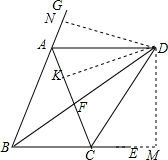
∴∠BDC=∠DCE-∠DBC=25°;
(2)∠BAC=2∠BDC,(或∠BDC=$\frac{1}{2}$∠BAC);
(3)过点D作DN⊥BA,DK⊥AC,DM⊥BC,垂足分别为点N、K、M.
∵BD、CD分别平分∠EBA、∠ECA,DN⊥BA,DK⊥AC,DM⊥BC,
∴DM=DN=DK,
∴AD平分∠GAC,∠ABD=∠DBC,
∴∠GAD=∠DAC,
∵∠GAC=∠ABC+∠ACB,
∴∠GAD=∠ABC,
∴AD∥BE.
点评 本题考查了等腰三角形的判定和性质,角平分线的性质,三角形的内角和,三角形的外角的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
7. 如图是由火柴棍搭成的几何图案,则第n个图案中的火柴棍的根数为(用含n的式子表示)( )
如图是由火柴棍搭成的几何图案,则第n个图案中的火柴棍的根数为(用含n的式子表示)( )
 如图是由火柴棍搭成的几何图案,则第n个图案中的火柴棍的根数为(用含n的式子表示)( )
如图是由火柴棍搭成的几何图案,则第n个图案中的火柴棍的根数为(用含n的式子表示)( )| A. | 4n | B. | 2n(n-1) | C. | 2n(n+1) | D. | 4n(n+2) |
8.下列各式的计算结果中,正确的是( )
| A. | 510×52=520 | B. | (-2ab3)3=8a3b9 | ||
| C. | x(2x+5)=2x2+5 | D. | (8x2y3-4x2y)÷2xy=4xy2-2x |
5.将二次函数y=$\frac{1}{4}$x2-3的图象向下平移2个单位长度后,所得图象的解析式是( )
| A. | y=$\frac{1}{4}$x2-5 | B. | y=$\frac{1}{4}$x2-3 | C. | y=$\frac{1}{4}$(x+2)2-3 | D. | y=$\frac{1}{4}$(x-2)2-3 |
12.下列说法中,正确的是( )
| A. | 近似数0.21与0.210的精确度相同 | B. | 数2.9951精确到百分位为3.00 | ||
| C. | 数轴上表示-a的点一定在原点左边 | D. | a-2的相反数是a+2 |
2.若不等式组$\left\{\begin{array}{l}{x≤2}\\{x>k}\end{array}\right.$有解,则k的取值范围是( )
| A. | k<2 | B. | k≥2 | C. | k<0 | D. | k≤0 |
9.一个凸多边形共有14条对角线,则这个多边形的边数是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
6.某商场一天中售出某品牌运动鞋13双,其中各种尺码的鞋的销售量如表所示,则这13双鞋的尺码组成的一组数据中,众数和中位数分别为( )
| 鞋的尺码(单位cm) | 23.5 | 24 | 24.5 | 25 | 25.5 | 26 |
| 销售量(单位:双) | 1 | 2 | 2 | 5 | 1 | 2 |
| A. | 25,25 | B. | 24.5,25 | C. | 26,25 | D. | 25,24.5 |
7.掷一枚质地均匀的正方体骰子,骰子的六个面上分别标有1、2、3、4、5、6的点数,掷得面朝上的点数为奇数的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |