题目内容
12.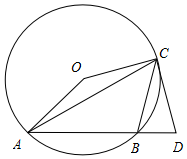 如图:△ABC是⊙O的内接三角形,∠ACB=45°,∠AOC=150°,过点C作⊙O的切线交AB的延长线于点D.
如图:△ABC是⊙O的内接三角形,∠ACB=45°,∠AOC=150°,过点C作⊙O的切线交AB的延长线于点D.(1)求证:CD=CB;
(2)如果⊙O的半径为$\sqrt{2}$,求AB的长.
分析 (1)首先连接OB,则∠AOB=2∠ACB=2×45°=90°,由∠AOC=150°,易得△OBC是等边三角形,又由过点C作⊙O的切线交AB的延长线于点D,易求得∠CBD=∠D=75°,继而证得结论;
(2)由(1)可得△AOB是等腰直角三角形,又由⊙O的半径为$\sqrt{2}$,即可求得答案.
解答 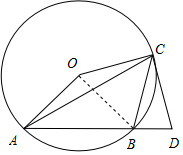 (1)证明:连接OB,则∠AOB=2∠ACB=2×45°=90°,
(1)证明:连接OB,则∠AOB=2∠ACB=2×45°=90°,
∵OA=OB,
∴∠OAB=OBA=45°,
∵∠AOC=150°,OA=OC,
∴∠OCA=∠OAC=15°,
∴∠OCB=∠OCA+∠ACB=60°,
∴△OBC是等边三角形,
∴∠BOC=∠OBC=60°,
∴∠CBD=180°-∠OBA-∠OBC=75°,
∵CD是⊙O的切线,
∴OC⊥CD,
∴∠D=360°-∠OBD-∠BOC-∠OCD=360°-(60°+75°)-60°-90°=75°,
∴∠CBD=∠D,
∴CB=CD;
(2)解:∵∠AOB=2∠ACB=90°,OA=OB=$\sqrt{2}$,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=2.
点评 此题考查了切线的性质、圆周角定理以及等腰直角三角形的性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
4.一个三角形的三边长都是整数,并且最长边是5,满足这些条件的三角形有( )
| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
2.在|-2|,-|0|,(-2)5,-|-2|,+(-2)中,负数共有( )
| A. | 1 个 | B. | 2个 | C. | 3个 | D. | 4个 |
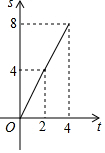
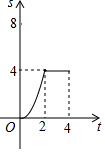
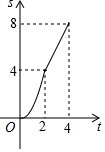
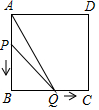 如图,在边长为4的正方形ABCD中,动点P从A点出发,以每秒1个单位长度的速度沿AB向B点运动,同时动点Q从B点出发,以每秒2个单位长度的速度沿BC→CD方向运动,当P运动到B点时,P、Q两点同时停止运动.设P点运动的时间为t秒,△APQ的面积为S,则表示S与t之间的函数关系的图象大致是( )
如图,在边长为4的正方形ABCD中,动点P从A点出发,以每秒1个单位长度的速度沿AB向B点运动,同时动点Q从B点出发,以每秒2个单位长度的速度沿BC→CD方向运动,当P运动到B点时,P、Q两点同时停止运动.设P点运动的时间为t秒,△APQ的面积为S,则表示S与t之间的函数关系的图象大致是( )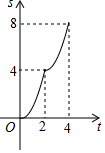
 如图是几个小立方块所搭几何体的俯视图,小正方形的数字表示该位置小立方块的个数.请画出这个几何体的主视图和左视图.
如图是几个小立方块所搭几何体的俯视图,小正方形的数字表示该位置小立方块的个数.请画出这个几何体的主视图和左视图.