题目内容
7.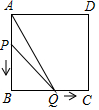 如图,在边长为4的正方形ABCD中,动点P从A点出发,以每秒1个单位长度的速度沿AB向B点运动,同时动点Q从B点出发,以每秒2个单位长度的速度沿BC→CD方向运动,当P运动到B点时,P、Q两点同时停止运动.设P点运动的时间为t秒,△APQ的面积为S,则表示S与t之间的函数关系的图象大致是( )
如图,在边长为4的正方形ABCD中,动点P从A点出发,以每秒1个单位长度的速度沿AB向B点运动,同时动点Q从B点出发,以每秒2个单位长度的速度沿BC→CD方向运动,当P运动到B点时,P、Q两点同时停止运动.设P点运动的时间为t秒,△APQ的面积为S,则表示S与t之间的函数关系的图象大致是( )| A. | 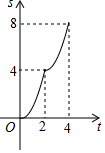 | B. | 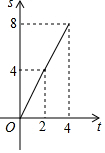 | C. | 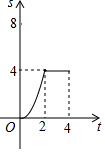 | D. | 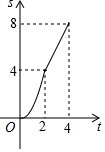 |
分析 根据动点P从A点出发,到B停止,速度为每秒1个单位,则时间为0~4秒,动点Q从B点出发,以每秒2个单位长度的速度沿BC→CD方向运动,路程为8,时间为0~4秒;
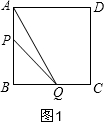
分两种情况:①当0<t≤2时,如图1,Q在BC上,则△APQ的面积为S=$\frac{1}{2}$AP•BQ=t2,图象为二次函数的抛物线;
②当2<t≤4时,如图2,点Q在CD上,其面积求得为2t,是一条直线;作出判断.
解答 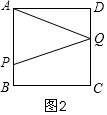
 解:分两种情况:
解:分两种情况:
①当0<t≤2时,如图1所示,
由题意得:AP=t,BQ=2t
S△APQ=$\frac{1}{2}$AP•BQ=$\frac{1}{2}$t•2t=t2,其图象是抛物线,
②当2<t≤4时,如图2所示,
S△APQ=$\frac{1}{2}$AP•BC=$\frac{1}{2}$×t×4=2t,其图象为一条直线,
故选D.
点评 本题是动点问题的函数图象,观察动点运动过程中所形成的△APQ的面积分为两类,采用了分类讨论的思想,结合图形与面积公式求出函数关系式,确定其函数类型,得出图象,作出正确判断.

练习册系列答案
相关题目
19.若3m=2,3n=5,则3m+n的值是( )
| A. | 7 | B. | 90 | C. | 10 | D. | a2b |
 对于有理数m,n,定义一种新运算,规定m?n=|m+n|-|m-n|
对于有理数m,n,定义一种新运算,规定m?n=|m+n|-|m-n|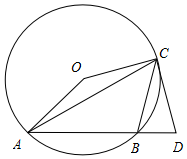 如图:△ABC是⊙O的内接三角形,∠ACB=45°,∠AOC=150°,过点C作⊙O的切线交AB的延长线于点D.
如图:△ABC是⊙O的内接三角形,∠ACB=45°,∠AOC=150°,过点C作⊙O的切线交AB的延长线于点D.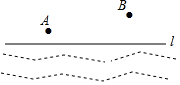 如图,L为汀江河的南岸线,一天傍晚某牧童在A处放牛,欲将牛牵到河边饮水后再回到家B处,牧童想以最短的路程回家.请你在图中画出牛饮水C的位置.(保留痕迹)
如图,L为汀江河的南岸线,一天傍晚某牧童在A处放牛,欲将牛牵到河边饮水后再回到家B处,牧童想以最短的路程回家.请你在图中画出牛饮水C的位置.(保留痕迹)