题目内容
3.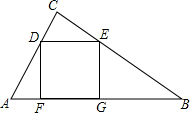 已知,如图,△ABC中,AC=3,BC=4,∠C=90°,四边形DEGF为正方形,其中D,E在边AC,BC上,F,G在AB上,求正方形的边长.
已知,如图,△ABC中,AC=3,BC=4,∠C=90°,四边形DEGF为正方形,其中D,E在边AC,BC上,F,G在AB上,求正方形的边长.(1)若将题中正方形改为矩形,DE=2DF,则矩形的边长为多少?(不需要计算结果,说说思路即可)
(2)若题中的三角形不是直角三角形,且AC=5,AB=11,BC=4$\sqrt{5}$,则正方形DEGF的边长为多少?
分析 作CN⊥AB于N,由四边形DEGF为正方形,可得CM⊥DE与求得AB、CN的值,还可证得△ABC∽△DEC,由相似三角形对应高的比等于相似比,即可求得正方形的边长;(1)作CN⊥AB,交DE于点M,交AB于点N,根据DE∥AB,得到△CDE∽△CAB,根据相似三角形的性质得到比例式,进而列出关于x的方程,求出方程的解,即可得到矩形的边长;
(2)如图1,作CN⊥AB,交GF于点M,交AB于点N,根据勾股定理列方程AC2-AN2=BC2-BN2,即25-AN2=80-(11-AN)2,求得AN=3,然后再由勾股定理得到CN=4,最后根据相似三角形的性质即可得到结论.
解答 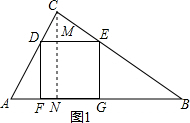 解:如图1,作CN⊥AB于N,
解:如图1,作CN⊥AB于N,
∵四边形DEGF为正方形,
∴CM⊥DE,
由勾股定理可得:AB=5,
根据三角形的面积不变性可求得CH=$\frac{12}{5}$,
设DE=x,
∵DE∥AB,
∴△ABC∽△DEC,
∴$\frac{CM}{CN}$=$\frac{DE}{AB}$,
即 $\frac{\frac{12}{5}-x}{\frac{12}{5}}=\frac{x}{5}$,
解得:x=$\frac{60}{37}$,
∴正方形的边长为:$\frac{60}{37}$;
(1)在图2中作CN⊥AB,交GF于点M,交AB于点N.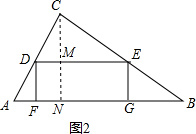
∵DE∥AB,
∴△CDE∽△CAB,
∴$\frac{CM}{CN}=\frac{DE}{AB}$,
设DF为x,则 DE=2x,
∴$\frac{\frac{12}{5}-x}{\frac{12}{5}}$=$\frac{2x}{5}$,
∴x=$\frac{60}{49}$;
∴矩形的边长为:DF=$\frac{60}{49}$,DE=$\frac{120}{49}$;
(2)如图1,作CN⊥AB,交DE于点M,交AB于点N,
∴AC2-AN2=BC2-BN2,
即25-AN2=80-(11-AN)2,
解得:AN=3,
∴CN=4,
∵DE∥AB,
∴△CDE∽△CAB,
∴$\frac{CM}{CN}=\frac{DE}{AB}$,
设正方形边长为x,
∴$\frac{4-x}{4}=\frac{x}{11}$,
解得:x=$\frac{44}{15}$,
∴正方形DEGF的边长为$\frac{44}{15}$.
点评 此题综合考查了正方形、矩形、相似三角形的性质及勾股定理.要求学生掌握相似三角形的对应高之比等于相似比.

 星级口算天天练系列答案
星级口算天天练系列答案| A. | $\frac{9}{4}$ | B. | $\frac{4}{9}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
 如图,梯形ABCD中,AD∥BC,AC⊥BD,垂足为H,∠DBE=∠CBE,BD=BC,求证:FH•AC=FC2+FC•FH.
如图,梯形ABCD中,AD∥BC,AC⊥BD,垂足为H,∠DBE=∠CBE,BD=BC,求证:FH•AC=FC2+FC•FH.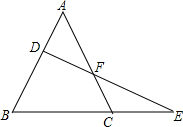 如图,△ABC中,直线DE交AB于D,交AC于F,交BC的延长线于E,求证:$\frac{AD}{DB}$•$\frac{BE}{EC}$•$\frac{CF}{FA}$=1.
如图,△ABC中,直线DE交AB于D,交AC于F,交BC的延长线于E,求证:$\frac{AD}{DB}$•$\frac{BE}{EC}$•$\frac{CF}{FA}$=1.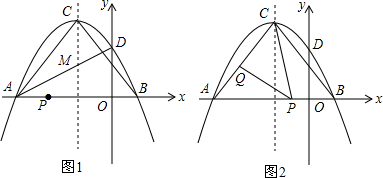
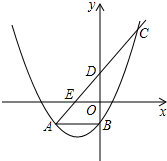 如图,抛物线y=ax2+2ax+c与直线y=x+b交于A(-2,-1)、C(1,2)两点,与y轴交于B,D、E是直线y=x+b与坐标轴的交点,
如图,抛物线y=ax2+2ax+c与直线y=x+b交于A(-2,-1)、C(1,2)两点,与y轴交于B,D、E是直线y=x+b与坐标轴的交点,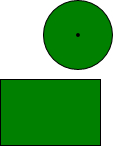 这是公园里两块形状不同的草坪,现在要修一条笔直的小路同时穿过这两块草坪,而且同时把两块草坪分成面积相同的两部分,如果你是设计师,你怎样设计这条小路?
这是公园里两块形状不同的草坪,现在要修一条笔直的小路同时穿过这两块草坪,而且同时把两块草坪分成面积相同的两部分,如果你是设计师,你怎样设计这条小路?