题目内容
在相似的两个三角形，已知其中一个三角形的三边长是4、6、8，另一个三角形最短的一边长是2，则另一个三角形的周长是（ ）
| A、4.5 | B、6 |
| C、9 | D、以上答案都有可能 |
考点：相似三角形的性质
专题：
分析：由一个三角形的三边长是4、6、8，即可求得此三角形的周长，又由相似三角形周长的比等于相似比，即可求得另一个三角形的周长．
解答：解：设另一个三角形的周长是x，
∵一个三角形的三边长是4、6、8，
∴这个三角形的周长为：4+6+8=18，
∵与它相似的另一个三角形最短的一边长是2，
∴
=
，
解得：x=9，
∴另一个三角形的周长是9．
故选C．
∵一个三角形的三边长是4、6、8，
∴这个三角形的周长为：4+6+8=18，
∵与它相似的另一个三角形最短的一边长是2，
∴
| x |
| 18 |
| 2 |
| 4 |
解得：x=9，
∴另一个三角形的周长是9．
故选C．
点评：此题考查了相似三角形的性质．解题的关键是注意掌握相似三角形周长的比等于相似比定理的应用．
练习册系列答案
相关题目
下列一组数：0.6，-4
，（-3）2，-5，-（-7）中负整数有（ ）
| 1 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
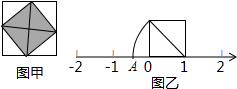根据图甲，在图乙的数轴上以1个单位长度的线段为边作一个正方形，以表示数1的点为圆心，以正方形对角线长为半径画弧，交数轴负半轴于点A，点A所表示的数是（ ）A、-1-
| ||
B、1-
| ||
C、
| ||
D、1-
|