题目内容
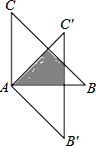 如图,△ABC绕点A顺时针旋转45°得到△A′B′C′,若∠BAC=90°,AB=AC=
如图,△ABC绕点A顺时针旋转45°得到△A′B′C′,若∠BAC=90°,AB=AC=| 2 |
考点:旋转的性质
专题:计算题
分析:先根据等腰直角三角形的性质得∠B=∠C=45°,再根据旋转的性质得∠BAC=45°,∠C′=∠C=45°,AC′=AC=
,于是可判断△AFC′为等腰直角三角形,∠AFC′=90°,则AF=
AC′=1,所以BF=AB-AF=
-1,接着判断△ABD和△BFE都是等腰三角形,则AD=BD=
AB=1,EF=BF=
-1,然后根据三角形面积公式和图中阴影部分的面积=S△ADB-S△BEF进行计算即可.
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| 2 |
解答: 解:∵∠BAC=90°,AB=AC=
解:∵∠BAC=90°,AB=AC=
,
∴∠B=∠C=45°,
∵△ABC绕点A顺时针旋转45°得到△A′B′C′,
∴∠BAC=45°,∠C′=∠C=45°,AC′=AC=
,
∴△AFC′为等腰直角三角形,∠AFC′=90°,
∴AF=
AC′=
×
=1,
∴BF=AB-AF=
-1,
∵∠BAD=∠B=45°,
∴△ABD和△BFE都是等腰三角形,
∴AD=BD=
AB=1,EF=BF=
-1,
∴图中阴影部分的面积=S△ADB-S△BEF=
×1×1-
×(
-1)2=
-1.
 解:∵∠BAC=90°,AB=AC=
解:∵∠BAC=90°,AB=AC=| 2 |
∴∠B=∠C=45°,
∵△ABC绕点A顺时针旋转45°得到△A′B′C′,
∴∠BAC=45°,∠C′=∠C=45°,AC′=AC=
| 2 |
∴△AFC′为等腰直角三角形,∠AFC′=90°,
∴AF=
| ||
| 2 |
| ||
| 2 |
| 2 |
∴BF=AB-AF=
| 2 |
∵∠BAD=∠B=45°,
∴△ABD和△BFE都是等腰三角形,
∴AD=BD=
| ||
| 2 |
| 2 |
∴图中阴影部分的面积=S△ADB-S△BEF=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.正确应用等腰直角三角形的性质是解决此题的关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
全面贯彻落实“大气十条”,抓好大气污染防治,是今年环保工作的重中之重.其中推进燃煤电厂脱硫改造15000 000千瓦是《政府工作报告》中确定的重点任务之一.将数据15 000 000用科学记数法表示为( )
| A、15×106 |
| B、1.5×107 |
| C、1.5×108 |
| D、0.15×108 |
 如图,DE∥AB,AD∥BC,求证:△EAD∽△ACB.
如图,DE∥AB,AD∥BC,求证:△EAD∽△ACB. 如图的图形是由一长方形及一等腰三角形所组成.
如图的图形是由一长方形及一等腰三角形所组成. 如图,AB是⊙O的直径,BC⊥AB,连接OC交⊙O于E点,弦AD∥OC,弦DF⊥AB于点G.
如图,AB是⊙O的直径,BC⊥AB,连接OC交⊙O于E点,弦AD∥OC,弦DF⊥AB于点G.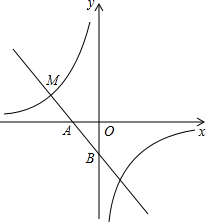 如图,一次函数y=-3x-1的图象与x轴交于点A,与y轴交于点B,与反比例函数y=
如图,一次函数y=-3x-1的图象与x轴交于点A,与y轴交于点B,与反比例函数y=