题目内容
1.已知抛物线的顶点为(1,-4),且过点(-2,5).(1)求抛物线解析式;
(2)求函数值y>0时,自变量x的取值范围.
分析 (1)由于已知抛物线顶点坐标,则可设顶点式y=a(x-1)2-4,然后把(-2,5)代入求出a的值即可;
(2)先求出抛物线与x轴的交点坐标,然后写出抛物线在x轴上方所对应的自变量的取值范围即可.
解答 解:(1)设抛物线解析式为y=a(x-1)2-4,
把(-2,5)代入得a•(-2-1)2-4=5,解得a=1,
所以抛物线解析式为y=(x-1)2-4,即y=x2-2x-3;
(2)当y=0时,x2-2x-3=0,解得x1=-1,x2=3,则抛物线与x轴的两交点坐标为(-1,0),(3,0),
而抛物线的开口向上,
所以当x<-1或x>3时,y>0.
点评 本题考查了待定系数法求二次函数的解析式:一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
相关题目
12.下列各数中是无理数的是( )
| A. | $\sqrt{2}$ | B. | 3.14 | C. | $\root{3}{8}$ | D. | $\frac{1}{3}$ |
9.若关于x的方程(a-1)x2+2x-1=0是一元二次方程,则a的取值范围是( )
| A. | a≠1 | B. | a>1 | C. | a<1 | D. | a≠0 |
16.将抛物线y=2x2-1,先向上平移2个单位,再向右平移1个单位后其顶点坐标是( )
| A. | (2,1) | B. | (1,2) | C. | (1,-1) | D. | (1,1) |
11.方程x2+2x+3=0的二次项系数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
 如图,四边形ABCD的对角线AC与BD相交于O点,∠1=∠2,∠3=∠4.
如图,四边形ABCD的对角线AC与BD相交于O点,∠1=∠2,∠3=∠4.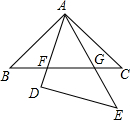 如图,△ABC与△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,△DEA绕点A旋转,边AD、AE与BC分别与AD、AE相交于点F、G,CB=5.回答下列问题.
如图,△ABC与△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,△DEA绕点A旋转,边AD、AE与BC分别与AD、AE相交于点F、G,CB=5.回答下列问题.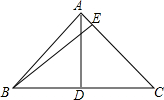 如图,在等腰△ABC中,AB=AC,底边上的高AD=10cm,腰AC上的高BE=12cm
如图,在等腰△ABC中,AB=AC,底边上的高AD=10cm,腰AC上的高BE=12cm