题目内容
11.化简下列各式,并把结果化为含有正整数指数幂的形式.(1)(2mn2)-2•(m-2n-1)-2;
(2)a-3b2•(a2b-2)-4÷(a-2b-1)2.
分析 (1)根据积的乘方,可得单项式的乘法,根据单项式的乘法,可得负整数指数幂,根据负整数指数幂与正整数指数幂互为倒数,可得答案;
(2)根据积的乘方,可得同底数幂的乘除法,根据同底数幂的乘除法,可得负整数指数幂,根据负整数指数幂与正整数指数幂互为倒数,可得答案.
解答 解:(1)原式=2-2m-2n-4•m4n2=$\frac{1}{2}$m2n-2=$\frac{{m}^{2}}{2{n}^{2}}$;
(2)原式=a-3b2•(a-8b8)÷(a-4b-2)=a-11b10÷(a-4b-2)=a-7b12=$\frac{{b}^{12}}{{a}^{7}}$.
点评 本题考查了负整数指数幂,熟记法则并根据法则计算是解题关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
6.计算($\frac{1}{2}$)-3的结果正确的是( )
| A. | -$\frac{1}{8}$ | B. | $\frac{1}{8}$ | C. | -8 | D. | 8 |
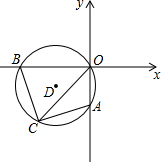 如图,在平面直角坐标系中,过原点的⊙D交坐标轴于A、B两点,且A(0,-2),OC平分∠AOB且交⊙D于点C,AC+BC=2$\sqrt{10}$.
如图,在平面直角坐标系中,过原点的⊙D交坐标轴于A、B两点,且A(0,-2),OC平分∠AOB且交⊙D于点C,AC+BC=2$\sqrt{10}$.