题目内容
2.甲、乙两站相距320千米,快车和慢车分别从甲、乙两站同时出发,反向而行.快车行驶140千米后,调头追赶慢车,在慢车驶离乙站1200千米处,快车追上慢车.已知快车每小时比慢车多行30千米.求快车和慢车的速度.分析 由题意可知:快车行驶的路程为140×2+320+1200=1800千米,慢车行驶的路程为1200千米,设慢车的速度为x千米/小时,则快车的速度为(x+30)千米/小时,根据行驶时间相等列出方程解答即可.
解答 解:设慢车的速度为x千米/小时,则快车的速度为(x+30)千米/小时,由题意得
$\frac{320+140×2+1200}{x+30}$=$\frac{1200}{x}$,
解得:x=60,
经检验x=60是原分式方程的解,
则x+30=90.
答:慢车的速度为60千米/小时,快车的速度为90千米/小时.
点评 此题考查分式方程的实际运用,掌握时间、速度、路程三者之间的关系是解决问题的根本,求得各自行驶的路程是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
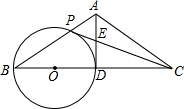 已知:如图,在等腰△ABC中,AB=AC,点D是边BC的中点,以BD为直径作⊙O,交边AB于点P,连接PC交AD于点E,且AE=DE.
已知:如图,在等腰△ABC中,AB=AC,点D是边BC的中点,以BD为直径作⊙O,交边AB于点P,连接PC交AD于点E,且AE=DE.