题目内容
 如图,在△ABC中,A、B、C三点的坐标分别为A(0,8),B(-6,0),C(15,0).若△ABC内心为D,则点D的坐标是
如图,在△ABC中,A、B、C三点的坐标分别为A(0,8),B(-6,0),C(15,0).若△ABC内心为D,则点D的坐标是考点:三角形的内切圆与内心,坐标与图形性质
专题:
分析:如图,作辅助线;运用圆的切线长定理求出CM的长度,进而求出OM的长度,此即点D的横坐标;运用三角形的面积公式求出DM的长度,此即点D的纵坐标.
解答: 解:如图,连接DA、DB、DC、DM、DN、DP;
解:如图,连接DA、DB、DC、DM、DN、DP;
∵⊙O为△ABC的内切圆,
∴AN=AP(设为λ),BM=BN(设为μ),CM=CP(设为γ);
DM⊥BC,DN⊥AB,DP⊥AC;
∵A、B、C三点的坐标分别为A(0,8),B(-6,0),C(15,0),
∴由勾股定理得:AB=10,AC=17,BC=21;
∴
,
解得γ=14,即CM=14,
∴OM=OC-CM=15-14=1;设⊙O的半径为φ;
∵△ABC的面积=△AOB、△AOC、△BOC的面积之和
∴由面积公式得:
BC•AO=
(AB+AC+BC)•θ,
解得:θ=
,即DM=
;
综上所述点D的坐标为(1,
).
故答案为:(1,
).
 解:如图,连接DA、DB、DC、DM、DN、DP;
解:如图,连接DA、DB、DC、DM、DN、DP;∵⊙O为△ABC的内切圆,
∴AN=AP(设为λ),BM=BN(设为μ),CM=CP(设为γ);
DM⊥BC,DN⊥AB,DP⊥AC;
∵A、B、C三点的坐标分别为A(0,8),B(-6,0),C(15,0),
∴由勾股定理得:AB=10,AC=17,BC=21;
∴
|
解得γ=14,即CM=14,
∴OM=OC-CM=15-14=1;设⊙O的半径为φ;
∵△ABC的面积=△AOB、△AOC、△BOC的面积之和
∴由面积公式得:
| 1 |
| 2 |
| 1 |
| 2 |
解得:θ=
| 7 |
| 2 |
| 7 |
| 2 |
综上所述点D的坐标为(1,
| 7 |
| 2 |
故答案为:(1,
| 7 |
| 2 |
点评:该题主要考查了三角形的内切圆的性质及其应用问题;解题的关键是作辅助线;灵活运用圆的切线长定理、内切圆的性质等几何知识点来分析、判断、推理或解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列命题中,是假命题的是( )
| A、同弧所对的圆周角相等 |
| B、同圆中相等的圆周角所对的弧相等 |
| C、等弧所对的圆周角相等或互补 |
| D、同圆中等弦所对的圆周角相等 |
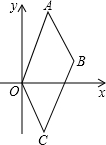 如图,在平面直角坐标系中,A(1,3)、B(2,1),四边形ABCD是平行四边形,求点C的坐标.
如图,在平面直角坐标系中,A(1,3)、B(2,1),四边形ABCD是平行四边形,求点C的坐标.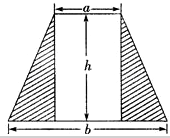 (1)用代数式表示图中阴影部分的面积S.
(1)用代数式表示图中阴影部分的面积S. 如图所示,CE是△ABC的外角∠ACF的平分线,CE交BA的延长线于点E,则∠BAC与∠B谁大?并说明理由.
如图所示,CE是△ABC的外角∠ACF的平分线,CE交BA的延长线于点E,则∠BAC与∠B谁大?并说明理由.