题目内容
1.计算:(1)$2\sqrt{2}({\sqrt{2}+\sqrt{\frac{1}{2}}})-\frac{{\sqrt{27}-\sqrt{12}}}{{\sqrt{3}}}$;
(2)$\frac{2}{3}\sqrt{9{x^3}}-{x^2}\sqrt{\frac{1}{x}}+10\sqrt{\frac{x}{4}}$.
分析 (1)先把各二次根式化为最简二次根式,然后合并后进行二次根式的乘除运算;
(2)先把各二次根式化为最简二次根式,然后合并即可.
解答 解:(1)原式=2$\sqrt{2}$($\sqrt{2}$+$\frac{\sqrt{2}}{2}$)-$\frac{3\sqrt{3}-2\sqrt{3}}{\sqrt{3}}$
=2$\sqrt{2}$•$\frac{3\sqrt{2}}{2}$-$\frac{\sqrt{3}}{\sqrt{3}}$
=6-1
=5;
(2)原式=2x$\sqrt{x}$-x$\sqrt{x}$+5$\sqrt{x}$
=(x+5)$\sqrt{x}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
 如图:已知AB∥DE∥CF,若∠ABC=60°,∠CDE=140°,求∠BCD的度数.
如图:已知AB∥DE∥CF,若∠ABC=60°,∠CDE=140°,求∠BCD的度数. 根据三视图求几何体的表面积.
根据三视图求几何体的表面积.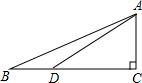 如图,AC⊥BC,cos∠ADC=$\frac{4}{5}$,tanB=$\frac{{\sqrt{3}}}{3}$,AD=10,求:(1)AC的长;(2)BD的长.
如图,AC⊥BC,cos∠ADC=$\frac{4}{5}$,tanB=$\frac{{\sqrt{3}}}{3}$,AD=10,求:(1)AC的长;(2)BD的长.