题目内容
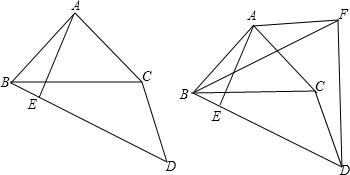
2. 如图,∠A=∠B,CE⊥AB,DF⊥AB,垂足分别为点E,F,且CE=DF,求证:AE=BF.
如图,∠A=∠B,CE⊥AB,DF⊥AB,垂足分别为点E,F,且CE=DF,求证:AE=BF.
分析 根据ASA可以证明△DFA≌△CEB得AF=BE即可证明.
解答  证明:∵CE⊥AB,DF⊥AB,
证明:∵CE⊥AB,DF⊥AB,
∴∠DFA=∠CEB=90°,
在△DFA或△CEB中,
$\left\{\begin{array}{l}{∠A=∠B}\\{∠DFA=∠CEB}\\{DF=CE}\end{array}\right.$,
∴△DFA≌△CEB(ASA),
∴AF=BE,
∴AE+EF=EF+FB,
∴AE=BF.
点评 本题考查全等三角形的判定和性质、线段的和差定义,熟练掌握全等三角形的判定是解决问题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
3.若|m-1|+(n+3)2=0,则(m-n)3的值为( )
| A. | 64 | B. | -6 | C. | 8 | D. | -8 |
11.一元二次方程x2-81=0的解是( )
| A. | x=-9 | B. | x=9 | C. | x1=9,x2=-9 | D. | x=81 |
9.已知点A(-2,y1),B(-1,y2),C(2,y3)是抛物线y=-(x-1)2+2上的三点,则y1,y2,y3的大小关系为( )
| A. | y1<y2<y3 | B. | y1>y2>y3 | C. | y1>y3>y2 | D. | y1<y3<y2 |