题目内容
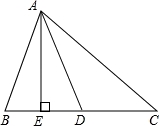
如图,若AE是△ABC边上的高,∠EAC的角平分线AD交BC于D,∠ACB=40°,求∠ADE.
【考点】三角形内角和定理;三角形的角平分线、中线和高.
【分析】根据直角三角形两锐角互余求出∠CAE,再根据角平分线的定义可得∠DAE= ∠CAE,进而得出∠ADE.
∠CAE,进而得出∠ADE.
【解答】解:∵AE是△ABC边上的高,∠ACB=40°,
∴∠CAE=90°﹣∠ACB=90°﹣40°=50°,
∴∠DAE= ∠CAE=
∠CAE= ×50°=25°,
×50°=25°,
∴∠ADE=65°.
【点评】本题考查了三角形的内角和定理,角平分线的定义,是基础题,熟记定理与概念并准确识图是解题的关键.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
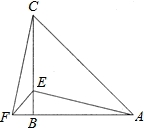
两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,AB=AC,AE=AD,∠BAC=∠EAD=90°,
| |
(1)请找出图2中与△ABE全等的三角形,并给予证明( 说明:结论中不得含
说明:结论中不得含
有未标识的字母);
 (2)求证:DC⊥BE.
(2)求证:DC⊥BE.
 D.3m
D.3m -2(a-2).
-2(a-2).
 化为一元二次方程的一般形式是__________,它的一次项系数是__________.
化为一元二次方程的一般形式是__________,它的一次项系数是__________.