Question

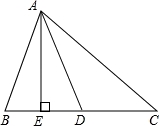
在△ABC中，AB=CB，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF．

（1）求证：Rt△ABE≌Rt△CBF；

（2）若∠CAE=30°，求∠ACF的度数．

 

Answer 1

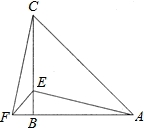
【考点】全等三角形的判定与性质．

【专题】几何图形问题；证明题；数形结合．

【分析】（1）由AB=CB，∠ABC=90°，AE=CF，即可利用HL证得Rt△ABE≌Rt△CBF；

（2）由AB=CB，∠ABC=90°，即可求得∠CAB与∠ACB的度数，即可得∠BAE的度数，又由Rt△ABE≌Rt△CBF，即可求得∠BCF的度数，则由∠ACF=∠BCF+∠ACB即可求得答案．

【解答】（1）证明：∵∠ABC=90°，

∴∠CBF=∠ABE=90°，

在Rt△ABE和Rt△CBF中，，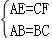

∴Rt△ABE≌Rt△CBF（HL）；

（2）解：∵AB=BC，∠ABC=90°，

∴∠CAB=∠ACB=45°，

又∵∠BAE=∠CAB﹣∠CAE=45°﹣30°=15°，

由（1）知：Rt△ABE≌Rt△CBF，

∴∠BCF=∠BAE=15°，

∴∠ACF=∠BCF+∠ACB=45°+15°=60°．

【点评】此题考查了直角三角形全等的判定与性质．此题难度不大，解题的关键是注意数形结合思想的应用．