题目内容
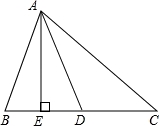
两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,AB=AC,AE=AD,∠BAC=∠EAD=90°,
| |
(1)请找出图2中与△ABE全等的三角形,并给予证明( 说明:结论中不得含
说明:结论中不得含
有未标识的字母);
 (2)求证:DC⊥BE.
(2)求证:DC⊥BE.
(5分)(1)解:△ABE≌△ACD,理由:………1分
∵∠BAC=∠EAD=90°
∴∠BAC+∠CAE=∠EAD+∠CAE
∴∠ ABE =∠ACD………1分
在△ABE与△ACD中
 ………2分
………2分
∴△ ABE≌△ACD (SAS) ………1分
ABE≌△ACD (SAS) ………1分
(4分)(2)证明:
∵△ABE≌△ACD
 ∴∠B=∠AC
∴∠B=∠AC D………1分
D………1分
∵∠BAC =90
∴∠ACB+∠B =90°
∴∠ACB+∠ACD =90°………1分
∴∠DCB =90°………1分
∴DC⊥BE………1分

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 B.
B. C.
C. D.
D.

 .7个
.7个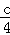 =0的根的情况是( )
=0的根的情况是( ) 1、2、﹣15 B.1、﹣2、﹣15 C.﹣1、﹣2、﹣15 D.﹣1、2、﹣15
1、2、﹣15 B.1、﹣2、﹣15 C.﹣1、﹣2、﹣15 D.﹣1、2、﹣15