题目内容
18.解下列方程组:(1)$\left\{\begin{array}{l}{3x-5z=6}\\{x+4z=-15}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{\frac{2x-1}{5}+\frac{3y-2}{4}=2}\\{\frac{3x+1}{5}-\frac{3y+2}{4}=0}\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{3x-5z=6①}\\{x+4z=-15②}\end{array}\right.$,
②×3-①得:17z=-51,即z=-3,
把z=-3代入②得:x=-3,
则方程组的解为$\left\{\begin{array}{l}{x=-3}\\{z=-3}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{8x+15y=54①}\\{12x-15y=6②}\end{array}\right.$,
①+②得:20x=60,即x=3,
把x=3代入①得:y=2,
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
8.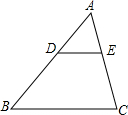 如图,△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,DE=2cm,则BC边的长是( )
如图,△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,DE=2cm,则BC边的长是( )
 如图,△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,DE=2cm,则BC边的长是( )
如图,△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,DE=2cm,则BC边的长是( )| A. | 6cm | B. | 4cm | C. | 8cm | D. | 7cm |
9. 如图所示几何体的俯视图是( )
如图所示几何体的俯视图是( )
 如图所示几何体的俯视图是( )
如图所示几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
13.近阶段潍坊持续干旱,给居民生活带来不便,关注水龙头的浪费十分必要,假设20滴水1毫升,一分钟浪费60滴,一年按365天计算,一年浪费水的质量用科学记数法表示为( )克(保留3个有效数字)
| A. | 1.60×106 | B. | 1.57×106 | C. | 1.58×106 | D. | 1.58×105 |
3.2015年某省遭遇历史罕见的夏秋东连旱,全省因灾造成直接经济损失68.77亿元,用科学记数法表示为( )
| A. | 68.77×109 | B. | 6.877×109 | C. | 6.877×1010 | D. | 6877×1010 |
7.在下列四个选项中,不适合普查的是( )
| A. | 了解全班同学每周体育锻炼的时间 | |
| B. | 鞋厂检查生产鞋底能承受的弯折次数 | |
| C. | 学校招聘新教师,对应聘教师面试 | |
| D. | 某中学调查九年级全体540名学生的平均身高 |
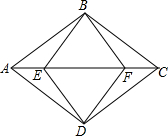 如图,ABCD是平行四边形,E、F是对角线AC上的两点,若∠ABF=∠CDE=90°.
如图,ABCD是平行四边形,E、F是对角线AC上的两点,若∠ABF=∠CDE=90°.