题目内容
4.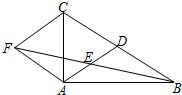 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
(3)在(2)问下当△ABC再满足一个什么条件,四边形ADCF为正方形.
分析 (1)连接DF,由AAS证明△AFE≌△DBE,得出AF=BD,即可得出答案;
(2)根据平行四边形的判定得出平行四边形ADCF,求出AD=CD,根据菱形的判定得出即可;
(3)根据等腰三角形性质求出AD⊥BC,得出∠ADC=90°,根据正方形的判定得出即可.
解答 (1)证明:连接DF,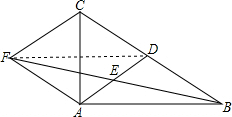
∵E为AD的中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠DBE,
在△AFE和△DBE中,
$\left\{\begin{array}{l}{∠AFE=∠DBE}\\{∠FEA=∠DEB}\\{AE=DE}\end{array}\right.$,
∴△AFE≌△DBE(AAS),
∴EF=BE,
∵AE=DE,
∴四边形AFDB是平行四边形,
∴BD=AF,
∵AD为中线,
∴DC=BD,
∴AF=DC;
(2)解:四边形ADCF的形状是菱形,理由如下:
∵AF=DC,AF∥BC,
∴四边形ADCF是平行四边形,
∵AC⊥AB,
∴∠CAB=90°,
∵AD为中线,
∴AD=$\frac{1}{2}$BC=DC,
∴平行四边形ADCF是菱形;
(3)解:当△ABC满足AC=AB时,四边形ADCF为正方形,理由如下:
∵∠CAB=90°,AC=AB,AD为中线,
∴AD⊥BC,
∴∠ADC=90°,
∵四边形ADCF是菱形,
∴四边形ADCF是正方形.
点评 本题考查了平行四边形的判定与性质,菱形、矩形、正方形的判定,全等三角形的性质和判定,直角三角形斜边上中线性质;本题综合性强,由一定难度,利于培养学生的推理能力.

练习册系列答案
相关题目
14.下面函数中,是正比例函数的是( )
| A. | y=6x | B. | y=$\frac{-6}{x}$ | C. | y=x2+6x | D. | y=3x-1 |
14.某校九年级一、二两个班共104人去春游,景区门票价格规定如下表:
设九年级一班的学生人数为x人
(Ⅰ)已知40<x<54,若两个班都以班为单位购票请根据表中提供的信息,用含有x的式子填写下表:
(Ⅱ)若x<50,两个班都以班为单位购票,共需1240元,求两个班各有多少学生?
(Ⅲ)在(Ⅱ)的条件下,若两个班联合起来购票,作为一个团体购票,可省多少钱?
| 购票张数 | 1~50张 | 51~100张 | 100张以上 |
| 每张票的价格 | 13元 | 11元 | 9元 |
(Ⅰ)已知40<x<54,若两个班都以班为单位购票请根据表中提供的信息,用含有x的式子填写下表:
| x=46 | 40<x≤50 | 50<x<54 | |
| 九年级一班购票费/元 | 13×46 | 13x | 11x |
| 九年级二班购票费/元 | 11×(104-46) | 11(104-x) | 11(104-x) |
(Ⅲ)在(Ⅱ)的条件下,若两个班联合起来购票,作为一个团体购票,可省多少钱?
 如图所示,点D为等边三角形ABC内的一点,BD=AD,BE=AB,∠DBE=∠DBC,则∠BED的度数是30度.
如图所示,点D为等边三角形ABC内的一点,BD=AD,BE=AB,∠DBE=∠DBC,则∠BED的度数是30度.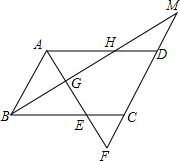 已知:如图,平行四边形ABCD中,AB=4,AD=6,∠A的平分线交BC于E,交DC延长线于点F,BG⊥AE,垂足为G,射线BG交AD于H,交CD延长线于M
已知:如图,平行四边形ABCD中,AB=4,AD=6,∠A的平分线交BC于E,交DC延长线于点F,BG⊥AE,垂足为G,射线BG交AD于H,交CD延长线于M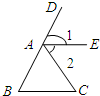 如图,AE平分∠CAD,且AE∥BC,给出下列结论:①∠1=∠2;②∠1=∠B;③∠2=∠C;④∠B=∠C;⑤∠C+∠BAE=180°.其中正确结论的个数有( )
如图,AE平分∠CAD,且AE∥BC,给出下列结论:①∠1=∠2;②∠1=∠B;③∠2=∠C;④∠B=∠C;⑤∠C+∠BAE=180°.其中正确结论的个数有( )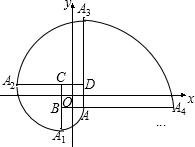 如图,在直角坐标系中,四边形ABCD是正方形,A(1,-1),B(-1,-1),C(-1,1),D(1,1).曲线AA1A2A3…叫做“正方形的渐开线”,其中弧AA1、弧A1A2、弧A2A3、弧A3A4…所在圆的圆心依次是点B、C、D、A循环,则点A2015坐标是(1,4031).
如图,在直角坐标系中,四边形ABCD是正方形,A(1,-1),B(-1,-1),C(-1,1),D(1,1).曲线AA1A2A3…叫做“正方形的渐开线”,其中弧AA1、弧A1A2、弧A2A3、弧A3A4…所在圆的圆心依次是点B、C、D、A循环,则点A2015坐标是(1,4031).