题目内容
 如图,正五边形ABCDE中,对角线AD,CE相交于F.求证:
如图,正五边形ABCDE中,对角线AD,CE相交于F.求证:(1)△AEF是等腰三角形;
(2)四边形ABCE是等腰梯形.
考点:等腰梯形的判定,等腰三角形的判定
专题:证明题
分析:(1)根据正五边形的内角和求得正五边形的各个角的度数,然后利用等腰三角形的性质求得△AEF的各个角的度数,根据等角对等边即可证得;
(2)根据(1)的计算,即可证明∠BAE+∠AEC=180°,即可证得AB∥CE,然后根据正多边形的定义证得.
(2)根据(1)的计算,即可证明∠BAE+∠AEC=180°,即可证得AB∥CE,然后根据正多边形的定义证得.
解答:证明:(1)∵五边形ABCDE是正五边形,
∴正五边形的各角都是180°-
=108°,
∵△CDE中,CD=DE,
∴∠CED=
=36°,
同理,∠DAE=36°,
∴∠AEC=108°-36°=72°,
∴∠AFE=180°-36°-72°=72°,
∴∠AEF=∠AFE,
∴AF=AE,即△AEF是等腰三角形;
(2)∵∠BAE+∠AEC=108°+72°=180°,
∴AB∥CE,
又∵BC=AE,
∴四边形ABCE是等腰梯形.
∴正五边形的各角都是180°-
| 360° |
| 5 |
∵△CDE中,CD=DE,
∴∠CED=
| 180°-108° |
| 2 |
同理,∠DAE=36°,
∴∠AEC=108°-36°=72°,
∴∠AFE=180°-36°-72°=72°,
∴∠AEF=∠AFE,
∴AF=AE,即△AEF是等腰三角形;
(2)∵∠BAE+∠AEC=108°+72°=180°,
∴AB∥CE,
又∵BC=AE,
∴四边形ABCE是等腰梯形.
点评:本题考查了正多边形的计算,以及等腰三角形的性质,和等腰梯形的定义,正确求得图中角的度数是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列计算错误的是( )
A、x6÷x-2=
| ||
| B、x2÷x6=x2 | ||
| C、(x-1y-2)-3=x3y6 | ||
| D、x9•x-9=1 |
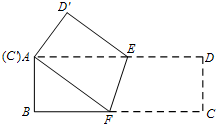 如图,将长方形纸片ABCD沿着EF折叠,使得点C与点A重合.
如图,将长方形纸片ABCD沿着EF折叠,使得点C与点A重合.