题目内容
已知正六边形的边心距为
,求该六边形外接圆的半径.
| 3 |
考点:正多边形和圆
专题:
分析:设正六边形的中心是O,一边是AB,过O作OG⊥AB与G,在直角△OAG中,根据三角函数即可求得边长AB,从而求出周长.
解答: 解:如图,在Rt△AOG中,OG=
解:如图,在Rt△AOG中,OG=
,∠AOG=30°,
∴OA=OG÷cos 30°=
÷
=2.
 解:如图,在Rt△AOG中,OG=
解:如图,在Rt△AOG中,OG=| 3 |
∴OA=OG÷cos 30°=
| 3 |
| ||
| 2 |
点评:本题主要考查正多边形的计算问题,常用的思路是转化为直角三角形中边和角的计算,属于常规题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
2015个同学站成一排报数,报出奇数的退出,偶数的留下;留下的同学位置不动重新报数,报到奇数的退出,偶数的留下…如此继续,最后留下一个同学,则最后留下的这个同学第一次站的位置是第( )
| A、256个 | B、512个 |
| C、1024个 | D、2013个 |
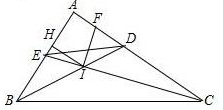 如图,△ABC中,∠A=90°,角平分线BD、CE交于点I,IF⊥CE交CA于F,IH⊥AB于H,下列结论:①∠DIF=45°;②CF+BE=BC;③AE+AF=2AH;④S四边形BEDC=2S△IBC,其中正确的结论为
如图,△ABC中,∠A=90°,角平分线BD、CE交于点I,IF⊥CE交CA于F,IH⊥AB于H,下列结论:①∠DIF=45°;②CF+BE=BC;③AE+AF=2AH;④S四边形BEDC=2S△IBC,其中正确的结论为 如图,正五边形ABCDE中,对角线AD,CE相交于F.求证:
如图,正五边形ABCDE中,对角线AD,CE相交于F.求证: 如图,△ABC中,∠BAC=90°,∠ABC=∠ACB,∠BDC=∠BCD,∠1=∠2,求∠3的度数.
如图,△ABC中,∠BAC=90°,∠ABC=∠ACB,∠BDC=∠BCD,∠1=∠2,求∠3的度数.