题目内容
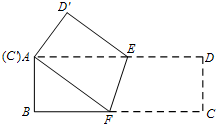 如图,将长方形纸片ABCD沿着EF折叠,使得点C与点A重合.
如图,将长方形纸片ABCD沿着EF折叠,使得点C与点A重合.(1)求证:AE=AF;
(2)若AB=3,BC=9,试求CF的长;
(3)在(2)的条件下,试求EF的长.
考点:翻折变换(折叠问题)
专题:
分析:(1)证明∠AFE=∠CFE;进而证明∠AEF=∠CFE,即可解决问题.
(2)根据勾股定理列出关于CF的方程,解方程,即可解决问题.
(3)证明AC⊥EF,此为解题的关键;求出AC的长度;借助面积公式即可解决问题.
(2)根据勾股定理列出关于CF的方程,解方程,即可解决问题.
(3)证明AC⊥EF,此为解题的关键;求出AC的长度;借助面积公式即可解决问题.
解答: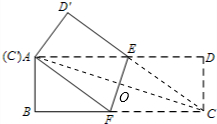 解:(1)由题意得:
解:(1)由题意得:
∠AFE=∠CFE;
∵AD∥BC,
∴∠AEF=∠CFE,
∴∠AEF=∠AFE,
∴AE=AF.
(2)由题意得:∠B=90°,AF=CF(设为x),
则BF=9-x;根据勾股定理得:x2=32+(9-x)2,
解得:x=5,即CF=5.
(3)如图,连接AC、CE.
由题意知:AC⊥EF;
由勾股定理得:CA2=32+92=90,
∴AC=3
;根据面积公式:
CF•AB=
AC•EF,
∴EF=
.
 解:(1)由题意得:
解:(1)由题意得:∠AFE=∠CFE;
∵AD∥BC,
∴∠AEF=∠CFE,
∴∠AEF=∠AFE,
∴AE=AF.
(2)由题意得:∠B=90°,AF=CF(设为x),
则BF=9-x;根据勾股定理得:x2=32+(9-x)2,
解得:x=5,即CF=5.
(3)如图,连接AC、CE.
由题意知:AC⊥EF;
由勾股定理得:CA2=32+92=90,
∴AC=3
| 10 |
CF•AB=
| 1 |
| 2 |
∴EF=
| 10 |
点评:该题主要考查了翻折变换的性质及其应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
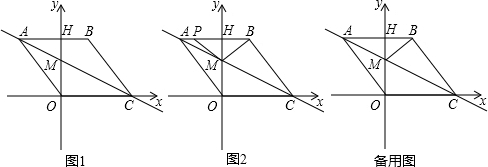
 如图,正五边形ABCDE中,对角线AD,CE相交于F.求证:
如图,正五边形ABCDE中,对角线AD,CE相交于F.求证: 直线y=kx+4与y轴交于点A,直线y=-2x+1与直线y=kx+4交于点B与y轴交于点C,点B的横坐标为-1.
直线y=kx+4与y轴交于点A,直线y=-2x+1与直线y=kx+4交于点B与y轴交于点C,点B的横坐标为-1.