题目内容
2.如图,某社会实践活动小组地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸点B在其北偏东45°方向,然后向西走60m到达C点,测得点B在点C的北偏东60°方向
(Ⅰ)求∠CBA的度数
(Ⅱ)求出这段河的宽(结果精确到1m,备用数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)

分析 (Ⅰ)根据题目中度数可以求得∠CBA的度数;
(Ⅱ)根据题意,作出合适的辅助线,然后根据锐角三角函数可以求得河宽,注意要精确到1m.
解答  解:(Ⅰ)作BD⊥AC于点D,
解:(Ⅰ)作BD⊥AC于点D,
由题意可得,
∠CBD=60°,∠ABD=45°,
∴∠CBA=∠CBD-∠ABD=15°;
(Ⅱ)由题意可得,
tan∠CBD=$\frac{CD}{BD}=\frac{60+AD}{BD}$,tan∠ABD=$\frac{AD}{BD}$
即$\sqrt{3}=\frac{60+CD}{BD}$,1=$\frac{AD}{BD}$,
解得,BD≈82,
即这段河的宽是82m.
点评 本题考查解直角三角形的应用-方向角问题,解答本题的关键是明确题意,找出所求问题需要的条件,利用锐角三角函数解答.

练习册系列答案
相关题目
14.已知实数x>0,实数y满足式子y=3-$\sqrt{{x}^{2}-2}+\sqrt{2-{x}^{2}}$,则x2y=( )
| A. | 0 | B. | 3 | C. | 6 | D. | 3$\sqrt{2}$ |
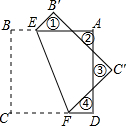 如图,正方形纸片ABCD的边长为8,E、F分别为AB、CD边上的点,将纸片沿EF折叠,求图中①②③④四个三角形的周长之和.
如图,正方形纸片ABCD的边长为8,E、F分别为AB、CD边上的点,将纸片沿EF折叠,求图中①②③④四个三角形的周长之和.
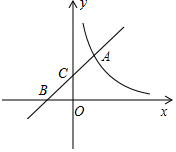 如图,直线y1=kx+2与反比例函数y2=$\frac{3}{x}$的图象交于点A(m,3),与坐标轴分别交于B,C两点.
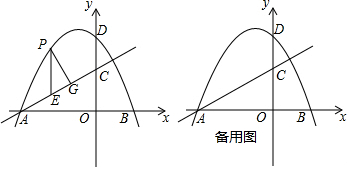
如图,直线y1=kx+2与反比例函数y2=$\frac{3}{x}$的图象交于点A(m,3),与坐标轴分别交于B,C两点. 如图,在平面直角坐标系中,抛物线y=-x2-2x+3与x轴交于A、C两点,与y轴交于点B,顶点为点D,已知点P(m,0)是线段CO上的动点,过点P作PQ⊥x轴交抛物线于点Q,交线段BC于点E,交直线CD于点F.
如图,在平面直角坐标系中,抛物线y=-x2-2x+3与x轴交于A、C两点,与y轴交于点B,顶点为点D,已知点P(m,0)是线段CO上的动点,过点P作PQ⊥x轴交抛物线于点Q,交线段BC于点E,交直线CD于点F.