题目内容
13．满足$\left\{\begin{array}{l}{2015≤x＜2025}\\{2015≤x+y+z＜2025}\\{2015≤x+2y+4z＜2025}\end{array}\right.$的不同的有序整数组（x，y，z）的个数为500．分析 分别求出x=2015、2016、…2024对应的y、z的值，即可得出答案．
解答 解：第一、当x=2015时，0≤y+z≤9，2y+4z≤9，
此时2y+4z取0，2，4，6，8，y+z取0，1，2，…，9，共50组；
第二、当x=2016时，-1≤y+z≤8，-1≤2y+4z≤8，
此时2y+4z取0，2，4，6，8，y+z取-1，0，…，8，共50组；
同理当x=2017、2018、…、2024，每种情况，有y、z恒有50种，
故共有500种，
故答案为：500．
点评 本题考查了不等式的整数解的应用，能根据求出结果得出规律是解此题的关键．
练习册系列答案
相关题目
若a、b、c在数轴上的对应点如图所示，化简|a+c|-|a+b|+|c-a|-|a-b|．
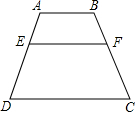如图，AB∥EF∥CD．
圆O的半径为1，P为圆周上一点，现将如图放置的边长为1的正三角形（实线所示，正三角形的顶点A和点P重合）沿着圆周顺时针滚动，经过若干次滚动，点A第一次回到点P的位置，则点A走过的路径所围成图形的面积为$\frac{2π}{3}$-$\sqrt{3}$．