题目内容
8.△ABC中,已知∠A,∠B,∠C的度数之比是1:2:3,BC=4,求△ABC的面积.分析 根据比例设∠A=k,∠B=2k,∠C=3k,然后根据三角形的内角和等于180°列方程求出k的值,从而得到三个内角的度数,再根据直角三角形30°角所对的直角边等于斜边的一半求出AB,利用勾股定理列式求出AC,然后根据三角形的面积公式列式计算即可得解.
解答 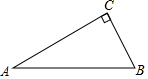 解:设∠A=k,∠B=2k,∠C=3k,
解:设∠A=k,∠B=2k,∠C=3k,
由三角形的内角和定理得,k+2k+3k=180°,
解得k=30°,
所以,∠A=30°,∠B=60°,∠C=90°,
∴AB=2BC=2×4=8,
由勾股定理得,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$,
所以,△ABC的面积=$\frac{1}{2}$AC•BC=$\frac{1}{2}$×4$\sqrt{3}$×4=8$\sqrt{3}$.
点评 本题考查了直角三角形30°角所对的直角边等于斜边的一半的性质,三角形的内角和定理,利用“设k法”求解三个内角的度数更简便.

练习册系列答案
相关题目
20.刘明上周买进股票1000股,每股27元,下表为本周每天该股票的涨跌情况.(单位:元)
(1)星期三收盘时,每股是多少元?
(2)若刘明按本周五的收盘价将股票全部卖出,你认为他会获利吗?获利多少?
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +1 | +1.5 | -1.5 | +2.5 | -0.5 |
(2)若刘明按本周五的收盘价将股票全部卖出,你认为他会获利吗?获利多少?

 如图,$\frac{BD}{BC}$=$\frac{BC}{AB}$=$\frac{CD}{AC}$=$\frac{3}{5}$,且△BDC的周长为12cm,求△ABC的周长.
如图,$\frac{BD}{BC}$=$\frac{BC}{AB}$=$\frac{CD}{AC}$=$\frac{3}{5}$,且△BDC的周长为12cm,求△ABC的周长. 如图,已知平行四边形ABCD及对角线BD,求作△BCD关于直线BD的对称图形(不要求写作法).
如图,已知平行四边形ABCD及对角线BD,求作△BCD关于直线BD的对称图形(不要求写作法).