题目内容
7.阅读并解答下列问题: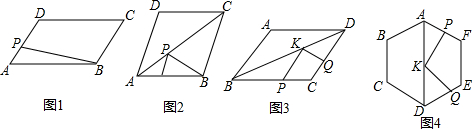
问题一:如图1,在?ABCD中,AD=4,AB=6,∠A=60°,点P是线段AD上的动点,连PB,当AP=3时,PB最小值为3$\sqrt{3}$.
问题二:如图2,四边形ABCD是边长为10的菱形,且∠DAB=60°,P是线段AC上的动点,E在AB上,且AE=$\frac{1}{2}$AB,连PE,PB,求PE+PB的最小值.
问题三:如图,菱形ABCD中,AB=10,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,求PK+QK的最小值.
问题四:如图3,正六边形ABCDEF中,AB=10,点P,Q,K分别为线段AF,DE,AD上任意的一点,则PK+QK的最小值为10$\sqrt{3}$.(写出答案即可)
分析 (1)如图1,过点B作BP⊥AD于P,根据直角三角形的性质和勾股定理就可以求出结论;
(2)连接BD,DE交AC与P点,由于四边形ABCD是边长为10的菱形,且∠DAB=60°,得到AC垂直平分BD,AB=AD=BD,DE即为PE+PB的最小值,根据菱形的性质,等边三角形的性质,得到DE的值,即得到结果;
(3)如图3,作点P关于直线BD的对称点P′,在菱形ABCD中,∵BD平分∠ABC,得到点P′落在边AB上,过点P′作P′Q⊥CD于Q,则P′Q的长度就是PK+QK的最小值,过点A作AE⊥CD于E,则四边形P′QEA是矩形,得到AE=P′Q,由∠BAC=120°,得到∠ADC=60°,AE=ADsin60°=10×$\frac{\sqrt{3}}{2}$=5$\sqrt{3}$,从而得到结果;
(4)如图4,在六边形ABCDEF中,AB∥DE,作点P关于直线AD的对称点P′,过P′作P′Q⊥DE于Q,则P′Q的长度就是PK+QK的最小值,连接BD,则四边形BDQP′是矩形,得到P′Q=BD,由∠BAF=120°,得到∠BAD=60°,BD=ABtan60°=10$\sqrt{3}$,于是得到结果.
解答 解::(1)如图1,过点B作BP⊥AD于P,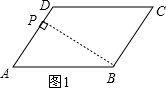
∴∠APB=90°.
∵∠A=60°,
∴∠ABP=30°,
∴AP=$\frac{1}{2}$AB,
∵AB=6,
∴AP=3.
在Rt△ABP中,由勾股定理,得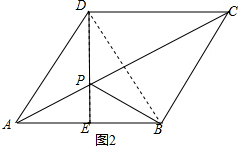 BP=$\sqrt{{(AB)}^{2}{-(AP)}^{2}}$=3$\sqrt{3}$
BP=$\sqrt{{(AB)}^{2}{-(AP)}^{2}}$=3$\sqrt{3}$
故答案:3,3$\sqrt{3}$;
(2)如图2,连接BD,DE交AC与P点,
∵四边形ABCD是边长为10的菱形,且∠DAB=60°,
∴AC垂直平分BD,AB=AD=BD,
∴DE即为PE+PB的最小值,
∵AE=$\frac{1}{2}$AB=5,
∴DE=$\sqrt{{AD}^{2}{-AE}^{2}}$=5$\sqrt{3}$,
即为PE+PB的最小值为:5$\sqrt{3}$;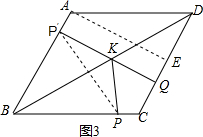 (3)如图3,作点P关于直线BD的对称点P′,
(3)如图3,作点P关于直线BD的对称点P′,
在菱形ABCD中,∵BD平分∠ABC,
∴点P′落在边AB上,过点P′作P′Q⊥CD于Q,
则P′Q的长度就是PK+QK的最小值,
过点A作AE⊥CD于E,
则四边形P′QEA是矩形,
∴AE=P′Q,
∵∠BAD=120°,
∴∠ADC=60°,
∵AD=10,
∴AE=ADsin60°=10×$\frac{\sqrt{3}}{2}$=5$\sqrt{3}$,
∴PK+QK=5$\sqrt{3}$;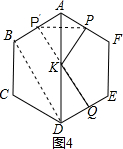
(4)如图4在六边形ABCDEF中,AB∥DE,
作点P关于直线AD的对称点P′,过P′作P′Q⊥DE于Q,
则P′Q的长度就是PK+QK的最小值,
连接BD,
则四边形BDQP′是矩形,
∴P′Q=BD,
∵∠BAF=120°,
∴∠BAD=60°,
∵AB=10,
∴BD=ABtan60°=10$\sqrt{3}$,
∴PK+QK=10$\sqrt{3}$.
故答案:10$\sqrt{3}$.
点评 本题考查的是最短路线问题,考查轴对称的性质的运用,全等三角形的判定及性质的运用,勾股定理的运用,等边三角形的性质的运用,解答(3)、(4)时作出P点关于直线对称的点P′是解答此题的关键.

| A. | 等边三角形 | B. | 平行四边形 | C. | 六边形 | D. | 圆 |
| A. | 20% | B. | 40% | C. | 60% | D. | 80% |
| A. | a3+a3=a6 | B. | (a+b)2=a2+b2 | C. | (ab)2=a2b2 | D. | a6÷a3=a2 |
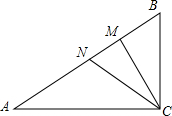 在Rt△ABC中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN=4.
在Rt△ABC中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN=4.