题目内容
17.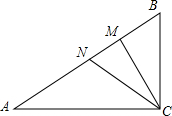 在Rt△ABC中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN=4.
在Rt△ABC中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN=4.
分析 由图示知:MN=AM+BN-AB,所以结合已知条件,根据勾股定理求出AC的长即可解答.
解答 解:在Rt△ABC中,根据勾股定理,AB=$\sqrt{1{2}^{2}+{5}^{2}}$=13,
又∵AC=12,BC=5,AM=AC,BN=BC,
∴AM=12,BN=5,
∴MN=AM+BN-AB=12+5-13=4.
故答案为:4.
点评 本题综合考查了勾股定理的应用,找到关系MN=AM+BN-AB是关键.

练习册系列答案
相关题目
8.在-3,-$\frac{1}{2}$,0,2四个数中,是负整数的是( )
| A. | -3 | B. | -$\frac{1}{2}$ | C. | 0 | D. | 2 |
2.七年级某班有男女同学若干人,女同学因故走了14名,这时男女同学之比为5:3,后来男同学又走了22名,这时男女同学人数相同,那么最初的女同学有( )
| A. | 39名 | B. | 43名 | C. | 47名 | D. | 55名 |
9.化简:(-m)12÷(-m)3等于( )
| A. | m4 | B. | -m4 | C. | m9 | D. | -m9 |
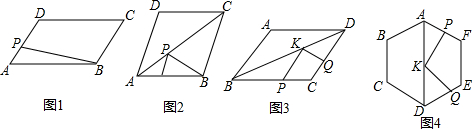
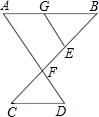 指出图中各对角的位置关系:
指出图中各对角的位置关系: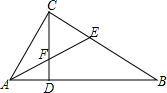 如图,△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠BAC交CD于F,交BC于E,试说明△CEF是等腰三角形.
如图,△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠BAC交CD于F,交BC于E,试说明△CEF是等腰三角形.