题目内容
4. 如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=30°,则∠ADE=30°.
如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=30°,则∠ADE=30°.
分析 先根据三角形内角和定理计算出∠B=60°,再根据折叠的性质得∠DEC=∠B=60°,然后根据三角形外角性质求∠ADE的度数.
解答 解:∵∠ACB=90°,∠A=30°,
∴∠B=90°-30°=60°,
∵沿CD折叠△CBD,使点B恰好落在AC边上的点E处,
∴∠DEC=∠B=60°,
∵∠DEC=∠A+∠ADE,
∴∠ADE=60°-30°=30°.
故答案为:30°.
点评 本题考查的是翻折变换和三角形内角和定理,三角形外角性质;理解翻折变换的性质、熟记三角形外角性质是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
14. 如图,AB是⊙O的直径,弦CD⊥AB于E,若OA=2,∠B=60°,则CD的长( )
如图,AB是⊙O的直径,弦CD⊥AB于E,若OA=2,∠B=60°,则CD的长( )
 如图,AB是⊙O的直径,弦CD⊥AB于E,若OA=2,∠B=60°,则CD的长( )
如图,AB是⊙O的直径,弦CD⊥AB于E,若OA=2,∠B=60°,则CD的长( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{5}$ | D. | 4 |
12.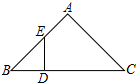 如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC交AB于点E,则有( )
如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC交AB于点E,则有( )
 如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC交AB于点E,则有( )
如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC交AB于点E,则有( )| A. | DE=DB | B. | DE=AE | C. | AE=BE | D. | AE=BD |
19.下面的几何体中,属于棱柱的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.下列方程是一元二次方程的是( )
| A. | $\sqrt{x+1}$ | B. | 2x(x-1)=2x2+3 | C. | $3x+\frac{1}{x}=4$ | D. | x2-2=0 |
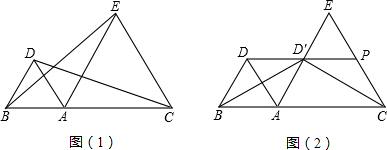
 有A,B,C三农户准备一起挖一口井,使它到三农户家的距离相等,这口井应挖在何处?请在图中标出井的位置,并说明理由.
有A,B,C三农户准备一起挖一口井,使它到三农户家的距离相等,这口井应挖在何处?请在图中标出井的位置,并说明理由.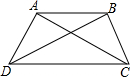 如图,AD=BC,∠ADC=∠BCD,求证:∠BAC=∠ABD.
如图,AD=BC,∠ADC=∠BCD,求证:∠BAC=∠ABD.